
【题目】已知曲线C1的参数方程为![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).
【答案】(1) ![]() ;(2) (
;(2) (![]() ),
),![]() .
.
【解析】试题分析:(1) 先根据同角三角函数关系cos2t+sin2t=1消参数得普通方程:(x-4)2+(y-5)2=25 ,再根据![]() 将普通方程化为极坐标方程:
将普通方程化为极坐标方程: ![]() (2)将
(2)将![]() 代入
代入![]() 得
得![]() 得
得![]() ,也可利用直角坐标方程求交点,再转化为极坐标
,也可利用直角坐标方程求交点,再转化为极坐标
试题解析: (1)∵C1的参数方程为![]()
∴(x-4)2+(y-5)2=25(cos2t+sin2t)=25,
即C1的直角坐标方程为(x-4)2+(y-5)2=25,
把![]() 代入(x-4)2+(y-5)2=25,
代入(x-4)2+(y-5)2=25,
化简得: ![]() .[Z.X.X.K]
.[Z.X.X.K]
(2)C2的直角坐标方程为x2+y2=2y,C1的直角坐标方程为(x-4)2+(y-5)2=25,
∴C1与C2交点的直角坐标为(1,1),(0,2).
∴C1与C2交点的极坐标为![]() .
.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:
【题目】已知向量![]() =(cosθ,sinθ),
=(cosθ,sinθ),![]() =(cosβ,sinβ).
=(cosβ,sinβ).
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 记f(θ)=
记f(θ)=![]() ,θ∈[0,
,θ∈[0,![]() ].当1≤λ≤2时,求f(θ)的最小值.
].当1≤λ≤2时,求f(θ)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+a|(a>-2)的图象过点(2,1).
(1)求实数a的值;
(2)设![]() ,在如图所示的平面直角坐标系中作出函数y=g(x)的简图,并写出(不需要证明)函数g(x)的定义域、奇偶性、单调区间、值域.
,在如图所示的平面直角坐标系中作出函数y=g(x)的简图,并写出(不需要证明)函数g(x)的定义域、奇偶性、单调区间、值域.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+2ax+3-b(a≠0,b>0)在[0,3]上有最小值2,最大值17,函数g(x)=![]() .
.
(l)求函数g(x)的解析式;
(2)证明:对任意实数m,都有g(m2+2)≥g(2|m|+l);
(3)若方程g(|log2x-1|)+3k(![]() -1)=0有四个不同的实数解,求实数k的取值范围.
-1)=0有四个不同的实数解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的周期为2,当x∈[0,2时,f(x)=2|x-1|-1,如果g(x)=f(x)-log3|x-2|,则函数y=g(x)的所有零点之和为( )
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程为![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面
的底面![]() 为菱形,
为菱形,![]() ,侧面
,侧面![]() 是边长为
是边长为![]() 的正三角形,侧面
的正三角形,侧面![]() 底面
底面![]() .
.
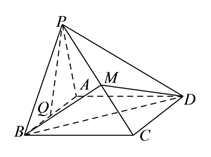
(![]() )设
)设![]() 的中点为
的中点为![]() ,求证:
,求证:![]() 平面
平面![]() .
.
(![]() )求斜线
)求斜线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(![]() )在侧棱
)在侧棱![]() 上存在一点
上存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )
A.56
B.60
C.120
D.140
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com