【答案】分析:由图表可猜想:第n行的连续的2n-1个数的和为:((n-1)2+1)+((n-1)2+2)+…+((n-1)2+2n-1)=(n-1)3+n3.
解答:解:∵等式的左边第一行一个数是1,为12;第二行三个数,为2,3,4,最后一个数是22;第三行五个数,为5,6,7,8,9,最后一个数是32,…
∴可猜想:第n-1行左端最后一个数是(n-1)2,右端为:(n-23+(n-1)3,
∴第n行左端第一个数是(n-1)2+1,有连续的2n-1个数相加,等式右端为:(n-1)3+n3,
即:((n-1)2+1)+((n-1)2+2)+…+((n-1)2+2n-1)=(n-1)3+n3.
证明:①当n=1时,左端=1=右端,等式成立;
②假设当n=k时等式成立,即((k-1)2+1)+((k-1)2+2)+…+((k-1)2+2k-1)=(k-1)3+k3,
则当n=k+1时,
([(k+1)-1]2+1)+([(k+1)-1]2+2)+…+([(k+1)-1]2+2k-1)+([(k+1)-1]2+2k)+([(k+1)-1]2+2k+1)
=[((k-1)2+1)+2(k-1)+1]+[((k-1)2+2)+2(k-1)+1]+…+[((k-1)2+2k-1)+2(k-1)+1]+([(k+1)-1]2+2k)+([(k+1)-1]2+2k+1)
=((k-1)2+1)+((k-1)2+2)+…+((k-1)2+2k-1)+[2(k-1)+1](2k-1)+([(k+1)-1]2+2k)+([(k+1)-1]2+2k+1)
=(k-1)3+k3+(2k-1)(2k-1)+k2+2k+k2+2k+1
=k3+[(k-1)3+6k2-4k+4k+2]
=k3+(k3-3k2+3k-1+6k2-4k+4k+2)
=k3+(k3+3k2+3k+1)
=k3+(k+1)3
=[(k+1)-1]3+(k+1)3.
即n=k+1时,等式也成立.
综合①②可知,对任意n∈N*,((n-1)2+1)+((n-1)2+2)+…+((n-1)2+2n-1)=(n-1)3+n3成立.
点评:本题考查数学归纳法,考查观察、猜想能力及论证推理能力,猜想出结论是关键,属于难题.

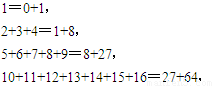 …;请你做出一般性的猜想,并且证明你猜想的结论.
…;请你做出一般性的猜想,并且证明你猜想的结论.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案