
【题目】某中学学校对高三年级文科学生进行了一次自主学习习惯的自评满意度的调查,按系统抽样方法得到了一个自评满意度(百分制,单位:分)的样本,如图分别是该样本数据的茎叶图和频率分布直方图(都有部分缺失).
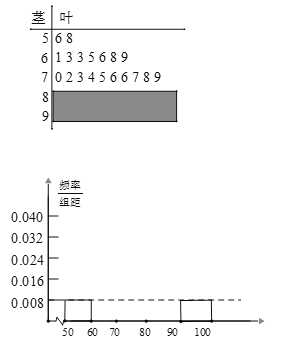
(1)完善频率分布直方图(需写出计算过程);
(2)分别根据茎叶图和频率分布直方图求出样本数据的中位数m1和m2,并指出选用哪一个数据来估计总体的中位数更合理(需要叙述理由).
【答案】(1)作图见解析(2)m1![]() 74;m2=73.5;用茎叶图得到的中位数估计总体的中位数更合理,详见解析
74;m2=73.5;用茎叶图得到的中位数估计总体的中位数更合理,详见解析
【解析】
(1)计算每个范围的频率,再完善频率分布图得到答案。
(2)分别计算中位数,判断茎叶图的中位数更合理。
(1)∵抽取的成绩在[50,60)的试卷份数是2份,频率是0.008×10=0.08,
∴一共抽取了![]() 25人.
25人.
∴抽取的成绩在[80,90)的试卷份数为:25﹣2﹣7﹣10﹣2=4份,
频率为![]() 0.16,
0.16,![]() 0.016;
0.016;
成绩在[70,80)的频率为![]() 0.4,
0.4,![]() 0.04;
0.04;
成绩在[60,70)的频率为![]() 0.28,
0.28,![]() 0.028;
0.028;
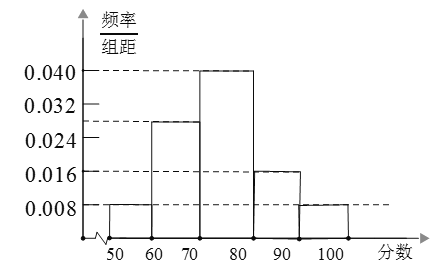
画出频率分布直方图如图所示;
(2)根据茎叶图计算样本数据的中位数是![]()
根据频率分布直方图求出样本数据的中位数是m2=70+10![]() 73.5;
73.5;
根据统计学原理知茎叶图保留了原始数据,它的中位数估计总体的中位数更合理.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P—ABC中,平面PAC⊥平面ABC,AB=BC,PA⊥PC.点E,F,O分别为线段PA,PB,AC的中点,点G是线段CO的中点.
(1)求证:FG∥平面EBO;
(2)求证:PA⊥BE.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为a,∠D=60°,点H为DC边中点,现以线段AH为折痕将△DAH折起使得点D到达点P的位置且平面PHA⊥平面ABCH,点E,F分别为AB,AP的中点.

(1)求证:平面PBC∥平面EFH;
(2)若三棱锥P﹣EFH的体积等于![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的短轴长为2,以椭圆
的短轴长为2,以椭圆![]() 的长轴为直径的圆与直线
的长轴为直径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,若直线
,若直线![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,求直线
为顶角的等腰直角三角形,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 经过点
经过点![]() ,且和直线
,且和直线![]() 相切.
相切.
(Ⅰ)求该动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,若斜率为1的直线
,若斜率为1的直线![]() 与线段
与线段![]() 相交(不经过坐标原点
相交(不经过坐标原点![]() 和点
和点![]() ),且与曲线
),且与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图判断闰年的流程图,判断公元1900年、公元2000年、公元2018年、公元2020年这四年中闰年的个数为(nMODm为n除以m的余数)( )
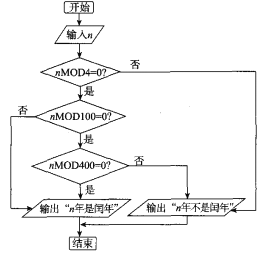
A.1个B.2个
C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
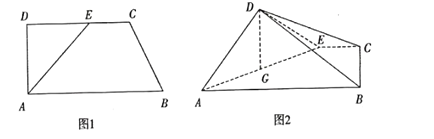
【题目】如图1,在直角梯形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (如图2).
(如图2).![]() 为
为![]() 中点
中点
(1)求证:![]() ;
;
(2)求四棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由
的值;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】互联网使我们的生活日益便捷,网络外卖也开始成为不少人日常生活中不可或缺的一部分,某市一调查机构针对该市市场占有率较高的甲、乙两家网络外卖企业(以下外卖甲、外卖乙)的经营情况进行了调查,调查结果如下表:
1日 | 2日 | 3日 | 4日 | 5日 | |
外卖甲日接单x(百单) | 5 | 2 | 9 | 8 | 11 |
外卖乙日接单y(百单) | 2 | 3 | 10 | 5 | 15 |
(1)试根据表格中这五天的日接单量情况,从统计的角度说明这两家外卖企业的经营状况;
(2)据统计表明,y与x之间具有线性关系.
①请用相关系数r对y与x之间的相关性强弱进行判断;(若![]() ,则可认为y与x有较强的线性相关关系(r值精确到0.001))
,则可认为y与x有较强的线性相关关系(r值精确到0.001))
②经计算求得y与x之间的回归方程为![]() ,假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于25百单时,外卖甲所获取的日纯利润的大致范围.(x值精确到0.01)
,假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于25百单时,外卖甲所获取的日纯利润的大致范围.(x值精确到0.01)
相关公式: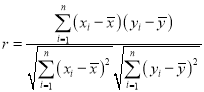 ,
,
参考数据: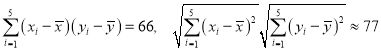 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上有解,求
上有解,求![]() 的取值范围;
的取值范围;
(3)设![]() 是函数
是函数![]() 的导函数,
的导函数,![]() 是函数
是函数![]() 的导函数,若函数
的导函数,若函数![]() 的零点为
的零点为![]() ,则点
,则点![]() 恰好就是该函数
恰好就是该函数![]() 的对称中心.试求
的对称中心.试求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com