练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】四棱锥P-ABCD中，底面ABCD为菱形，且，侧面PAD是正三角形，其所在的平面垂直于底面ABCD，点G为AD的中点.

    （1）求证：BG面PAD；

    （2）E是BC的中点，在PC上求一点F，使得PG面DEF.

    【答案】（1）证明见解析；（2）F为PC中点时满足题意，具体见解析

    【解析】

    （1）连结BD，证明BGAD，因为面PAD底面ABCD，且面PAD底面ABCD=AD，即可证明BG垂直于面PAD；

    （2）点E是 BC的中点，点F为PC的中点，连接GC交DE于点H，证明PGFH ，因为面DEF，面DEF，即可证明PG面DEF.

    证明：（1）连结BD，因为四边形ABCD为菱形，且，

    所以三角形ABD为正三角形，又因为点G为AD的中点，所以BGAD；

    因为面PAD底面ABCD，且面PAD底面ABCD=AD，

    平面，

    所以BG面PAD.

    （2）当点F为PC的中点时，PG面DEF，

    连结GC交DE于点H，

    因为E、G分别为菱形ABCD的边BC、AD的中点，所以四边形DGEC为平行四边形，

    所以点H为DE的中点，又点F为PC的中点，

    所以FH是三角形PGC的中位线，所以PGFH ，

    因为面DEF，面DEF，

    所以PG面DEF.

    综上：当点F为PC的中点时，PG面DEF.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】海南盛产各种名贵树木，如紫檀、黄花梨等.在实际测量单根原木材体积时，可以检量木材的实际长度（检尺长）和小头直径（检尺径），再通过国家公布的原木材积表直接查询得到，原木材积表的部分数据如下所示：

    检尺径

    （）

    检尺长（）

    2.0

    2.2

    2.4

    2.5

    2.6

    材积（）

    8

    0.0130

    0.0150

    0.0160

    0.0170

    0.0180

    10

    0.0190

    0.0220

    0.0240

    0.0250

    0.0260

    12

    0.0270

    0.0300

    0.0330

    0.0350

    0.0370

    14

    0.0360

    0.0400

    0.0450

    0.0470

    0.0490

    16

    0.0470

    0.0520

    0.0580

    0.0600

    0.0630

    18

    0.0590

    0.0650

    0.0720

    0.0760

    0.0790

    20

    0.0720

    0.0800

    0.0880

    0.0920

    0.0970

    22

    0.0860

    0.0960

    0.1060

    0.1110

    0.1160

    24

    0.1020

    0.1140

    0.1250

    0.1310

    0.1370

    若小李购买了两根紫檀原木，一根检尺长为，检尺径为，另一根检尺长为，检尺径为，根据上表，可知两根原木的材积之和为______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列的公差为，前n项和为，且满足____________.（从①）；②成等比数列；③，这三个条件中任选两个补充到题干中的横线位置，并根据你的选择解决问题）

    （I）求；

    （Ⅱ）若，求数列的前n项和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆，A为C的上顶点，过A的直线l与C交于另一点B，与x轴交于点D，O点为坐标原点．

    （1）若，求l的方程；

    （2）已知P为AB的中点，y轴上是否存在定点Q，使得？若存在，求Q的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,在多面体ABCDE中,DE∥AB,AC⊥BC,BC＝2AC＝2,AB＝2DE,且D点在平面ABC内的正投影为AC的中点H且DH＝1．

    （1）证明：面BCE⊥面ABC

    （2）求BD与面CDE夹角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

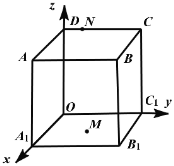
    【题目】单位正方体在空间直角坐标系中的位置如图所示，动点，，其中，，设由，，三点确定的平面截该正方体的截面为，那么（ ）

    A.对任意点，存在点使截面为三角形

    B.对任意点，存在点使截面为正方形

    C.对任意点和，截面都为梯形

    D.对任意点，存在点使得截面为矩形

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线C的参数方程为（为参数），以平面直角坐标系的原点O为极点，x轴正半轴为极轴建立极坐标系.

    （1）求曲线C的极坐标方程；

    （2）过点，倾斜角为的直线l与曲线C相交于M，N两点，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，的导函数为.

    （1）当时，证明：函数在上单调递增；

    （2）若，讨论函数零点的个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面是边长为2的正方形，，为中点，点在上且平面，在延长线上，，交于，且

    (1)证明：平面；

    (2)设点在线段上，若二面角为，求的长度．

    查看答案和解析>>

    同步练习册答案