
【题目】设f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值.求实数a的取值范围.
【答案】(Ⅰ)当![]() 时,函数
时,函数![]() 单调递增区间为
单调递增区间为![]() ,当
,当![]() 时,函数
时,函数![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ; (Ⅱ)
; (Ⅱ)![]()
【解析】试题分析:(Ⅰ)先求出![]() ,然后讨论当
,然后讨论当![]() 时,当
时,当![]() 时的两种情况即得.
时的两种情况即得.
(Ⅱ)分以下情况讨论:①当![]() 时,②当
时,②当![]() 时,③当
时,③当![]() 时,④当
时,④当![]() 时,综合即得.
时,综合即得.
试题解析:(Ⅰ)由![]()
可得![]() ,
,
则![]() ,
,
当![]() 时,
时,
![]() 时,
时, ![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() 时,
时,
![]() 时,
时, ![]() ,函数
,函数![]() 单调递增,
单调递增,
![]() 时,
时, ![]() ,函数
,函数![]() 单调递减.
单调递减.
所以当![]() 时,
时, ![]() 单调递增区间为
单调递增区间为![]() ;
;
当![]() 时,函数
时,函数![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(Ⅱ)由(Ⅰ)知, ![]() .
.
①当![]() 时,
时, ![]() ,
, ![]() 单调递减.
单调递减.
所以当![]() 时,
时, ![]() ,
, ![]() 单调递减.
单调递减.
当![]() 时,
时, ![]() ,
, ![]() 单调递增.
单调递增.
所以![]() 在x=1处取得极小值,不合题意.
在x=1处取得极小值,不合题意.
②当![]() 时,
时, ![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() 在
在![]() 内单调递增,
内单调递增,
可得当当![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
所以![]() 在(0,1)内单调递减,在
在(0,1)内单调递减,在![]() 内单调递增,
内单调递增,
所以![]() 在x=1处取得极小值,不合题意.
在x=1处取得极小值,不合题意.
③当![]() 时,即
时,即![]() 时,
时, ![]() 在(0,1)内单调递增,在
在(0,1)内单调递增,在![]() 内单调递减,
内单调递减,
所以当![]() 时,
时, ![]() ,
, ![]() 单调递减,不合题意.
单调递减,不合题意.
④当![]() 时,即
时,即![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
当![]() 时,
时, ![]() ,
, ![]() 单调递减,
单调递减,
所以f(x)在x=1处取得极大值,合题意.
综上可知,实数a的取值范围为![]() .
.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左右顶点分别是
的左右顶点分别是![]() ,
,![]() 为直线
为直线![]() 上一点(
上一点(![]() 点在
点在![]() 轴的上方),直线
轴的上方),直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() ,直线
,直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() .
.

(1)若![]() 的面积是
的面积是![]() 的面积的
的面积的![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线![]() 与直线
与直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)若![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,△ABC是以BC为斜边的等腰直角三角形,△BCD是边长为2的正三角形.

(Ⅰ)当AD为多长时,![]() ?
?
(Ⅱ)当二面角B﹣AC﹣D为![]() 时,求AD的长.
时,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市有一直角梯形绿地ABCD,其中∠ABC=∠BAD=90°,AD=DC=2km,BC=1km.现过边界CD上的点E处铺设一条直的灌溉水管EF,将绿地分成面积相等的两部分. 
(1)如图①,若E为CD的中点,F在边界AB上,求灌溉水管EF的长度;
(2)如图②,若F在边界AD上,求灌溉水管EF的最短长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校随机调查80名学生,以研究学生爱好羽毛球运动与性别的关系,得到下面的![]() 列联表:
列联表:
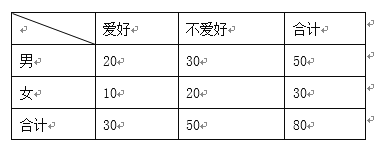
(1)将此样本的频率视为总体的概率,随机调查本校的3名学生,设这3人中爱好羽毛球运动的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)根据表3中数据,能否认为爱好羽毛球运动与性别有关?
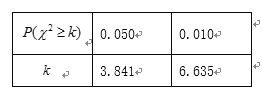
附:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣(x﹣2m)(x+m+3)(其中m<﹣1),g(x)=2x﹣2.
(1)若命题“log2g(x)<1”是真命题,求x的取值范围;
g(x)<0.若p∧q是真命题,求m的取值范围.
(2)设命题p:x∈(1,+∞),f(x)<0或g(x)<0;命题q:x∈(﹣1,0),f(x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的平均数、众数和中位数;
(3)在月平均用电量为,![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在
的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了政府对过热的房地产市场进行调控决策,统计部门对城市人和农村人进行了买房心理预测调研,用简单随机抽样的方法抽取了110人进行统计,得到如下列联表:
买房 | 不买房 | 纠结 | |
城市人 | 5 | 15 | |
农村人 | 20 | 10 |
已知样本中城市人数与农村人数之比是3:8.
(Ⅰ)分别求样本中城市人中的不买房人数和农村人中的纠结人数;
(Ⅱ)从参与调研的城市人中用分层抽样方法抽取6人,进一步统计城市人的某项收入指标,假设一个买房人的指标算作3,一个纠结人的指标算作2,一个不买房人的指标算作1,现在从这6人中再随机选取3人,令X=再抽取3人指标之和,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com