练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

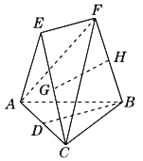
    【题目】在如图所示的几何体中，是的中点，.

    （1）已知，，求证：平面；

    （2）已知分别是和的中点，求证：平面.

    【答案】（1）详见解析；（2）详见解析.

    【解析】试题分析：（1）根据,所以平面就是平面,连接DF,AC是等腰三角形ABC和ACF的公共底边，点D是AC的中点，所以,,即证得平面的条件；（2）要证明线面平行，可先证明面面平行，取的中点为，连接，，根据中位线证明平面平面,即可证明结论.

    试题解析：证明：（1）∵，∴与确定平面.

    如图①，连结. ∵，是的中点，∴.同理可得.

    又，平面，∴平面，即平面.

    （2）如图②，设的中点为，连接，.

    在中，∵分别是的中点，∴.

    又，∴.

    在中，∵分别是的中点，∴.

    又，∴平面平面.

    ∵平面，∴平面.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】以下四个命题中：

    ①在回归分析中, 可用相关指数的值判断的拟合效果,越大,模型的拟合效果越好；

    ②两个随机变量的线性相关性越强,相关系数的绝对值越接近；

    ③若数据的方差为,则的方差为；

    ④对分类变量与的随机变量的观测值来说, 越小,判断“与有关系”的把握程度越大．

    其中真命题的个数为（ ）

    A． B． C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，C、F是⊙O上的两点，OC⊥AB，过点F作⊙O的切线FD交AB的延长线于点D．连接CF交AB于点E．

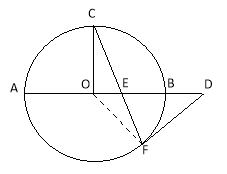
    （1）求证：DE2=DBDA；

    （2）若DB=2，DF=4，试求CE的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，以椭圆的四个顶点为顶点的四边形的面积为．

    （1）求椭圆的方程；

    （2）斜率为的直线过椭圆的右焦点，且与椭圆交与两点，过线段的中点与垂直的直线交直线于点，若为等边三角形，求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着“银发浪潮”的涌来，养老是当下普遍关注的热点和难点问题，某市创新性的采用“公建民营”的模式，建立标准的“日间照料中心”，既吸引社会力量广泛参与养老建设，也方便规范化管理，计划从中抽取5个中心进行评估，现将所有中心随机编号，用系统（等距）抽样的方法抽取，已知抽取到的号码有5号23号和29号，则下面号码中可能被抽到的号码是（ ）

    A. 9 B. 12 C. 15 D. 17

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形是平行四边形，平面，，，，，，，为的中点.

    （1）求证：平面；

    （2）求证：平面平面；

    （3）求多面体的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

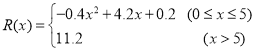    【题目】甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律：每生产产品（百台），其总成本为（万元），其中固定成本为2万元，并且每生产1百台的生产成本为1万元（总成本固定成本+生产成本），销售收入，假定该产品产销平衡（即生产的产品都能卖掉），根据上述统计规律，请完成下列问题

    （1）写出利润函数的解析式（利润销售收入—总成本）；

    （2）甲厂生产多少台新产品时，可使盈利最多？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，，圆是以的中点为圆心，为半径的圆.

    （1）若圆的切线在轴和轴上截距相等，求切线方程；

    （2）若是圆外一点，从向圆引切线，为切点，为坐标原点，，求使最小的点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）当时，求证：；

    （2）当函数与函数有且仅有一个交点，求的值；

    （3）讨论函数的零点个数.

    查看答案和解析>>

    同步练习册答案