
分析 根据[x]的定义,分别可以求出x∈(-2.5,-2),[-2,-1),[-1,0),[0,1),[1,2),以及x=2时的[x]的取值,从而便可得出函数f(x)的值域.
解答 解:x∈(-2.5,-2)时,[x]=-3,x∈[-2,-1)时,[x]=-2,x∈[-1,0)时,[x]=-1,x∈[0,1)时,[x]=0,x∈[1,2)时,[x]=1,x=2时,[x]=2;
∴x∈(-2.5,2]时,[x]的取值为:-3,-2,-1,0,1,2;
∴f(x)的值域为{-3,-2,-1,0,1,2}.
故答案为:{-3,-2,-1,0,1,2}.
点评 考查函数值域的概念,以及对[x]定义的理解,通过本题可以看出x∈(-2.5,2]时,[x]便是区间(-2.5,2]之间的整数,再加上不超过端点值的最大整数,便是所有[x]在(-2.5,2]上的取值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 锐角三角形 | ||
| C. | 钝角三角形 | D. | 直角或钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
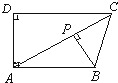 如图,已知四边形ABCD中AB∥CD,AD⊥AB,BP⊥AC,BP=PC,CD>AB,则经过某种翻折后以下线段可能会相互重合的是( )
如图,已知四边形ABCD中AB∥CD,AD⊥AB,BP⊥AC,BP=PC,CD>AB,则经过某种翻折后以下线段可能会相互重合的是( )| A. | AB与AD | B. | AB与BC | C. | BD与BC | D. | AD与AP |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{π}{3}$] | B. | [$\frac{π}{3}$,$\frac{π}{2}$) | C. | [$\frac{π}{6}$,$\frac{π}{3}$] | D. | ($\frac{π}{4}$,$\frac{π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
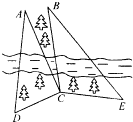 如图,为了开发某森林区,某测量人员身处这个森林区一条河的南岸,为了测量河对岸不能到达的两点A,B之间的距离,同时由于树木的遮挡,不可能分别在两个不同地点同时观察到点A,B;但她在南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;已知A,B,C,D,E在同一水平面内并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(km).
如图,为了开发某森林区,某测量人员身处这个森林区一条河的南岸,为了测量河对岸不能到达的两点A,B之间的距离,同时由于树木的遮挡,不可能分别在两个不同地点同时观察到点A,B;但她在南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;已知A,B,C,D,E在同一水平面内并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(km).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com