
若数列 满足:存在正整数
满足:存在正整数 ,对于任意正整数
,对于任意正整数 都有
都有 成立,则称数列
成立,则称数列 为周期数列,周期为
为周期数列,周期为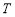 . 已知数列
. 已知数列 满足
满足 ,
,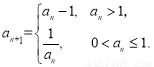 现给出以下命题:
现给出以下命题:
①若 ,则
,则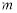 可以取3个不同的值
可以取3个不同的值
②若 ,则数列
,则数列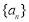 是周期为
是周期为 的数列
的数列
③ 且
且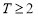 ,存在
,存在 ,
, 是周期为
是周期为 的数列
的数列
④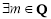 且
且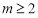 ,数列
,数列 是周期数列.其中所有真命题的序号是 .
是周期数列.其中所有真命题的序号是 .
①②③
【解析】对于①,根据条件,当m>2时,有a2=m-1>1,a3=m-2,于是m-2=4,有m=6满足条件;当m∈(1,2]时,有a2=m-1∈(0,1],则a3=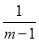 ,于是
,于是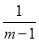 =4,m=
=4,m=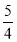 满足条件;若m=1,则an=1恒成立,不可能有a3=4,当m∈(0,1)时,有a2=
满足条件;若m=1,则an=1恒成立,不可能有a3=4,当m∈(0,1)时,有a2=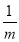 >1,a3=
>1,a3=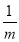 -1,于是
-1,于是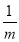 -1=4,m=
-1=4,m= 满足条件.故①正确.
满足条件.故①正确.
对于②,逐个推导可得:a1=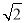 ,a2=
,a2=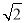 -1,a3=
-1,a3=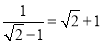 ,a4=
,a4=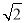 , 是周期为3的周期数列.故②正确
, 是周期为3的周期数列.故②正确
对于③,要想使得{an}是周期为T的周期数列,因为m>1,故只需使得aT=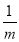 ,则aT+1=m,而m>1,可使得aT=m-(T-1),即m-(T-1)=
,则aT+1=m,而m>1,可使得aT=m-(T-1),即m-(T-1)=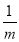 ,于是m2-(T-1)m-1=0,该关于m的方程两根之积为-1,必为异号两根,而根之和为T-1≥1,故其正根m必定大于1,满足条件,故③正确;
,于是m2-(T-1)m-1=0,该关于m的方程两根之积为-1,必为异号两根,而根之和为T-1≥1,故其正根m必定大于1,满足条件,故③正确;
对于④,仿照③可知,当T=1时,m=1不满足条件
当T∈N*且T≥2时,若m为整数,则必定在若干项以后出现an=1,之后成为常数数列,不合题意,
故m为非整数,且m=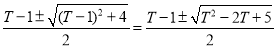 (舍负),
(舍负),
要使得m∈Q,则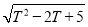 必为有理数(且为整数),令其为n,且T-1+n不是偶数,否则m为整数,即T+n是偶数,所以,T与n同奇或同偶
必为有理数(且为整数),令其为n,且T-1+n不是偶数,否则m为整数,即T+n是偶数,所以,T与n同奇或同偶
由T2-2T+5=n2知,T与n不能同为偶数,
当T为奇数时,T2是奇数,等式左边是偶数,这与n2为奇数矛盾
综上,这样的条件不可能满足.故④错误
考点:分段数列,周期性,数列综合问题


科目:高中数学 来源:2013-2014学年山东省菏泽市高三3月模拟考试文科数学试卷(解析版) 题型:解答题
如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且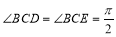 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
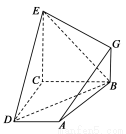
(1)求证: EC⊥CD ;
(2)求证:AG∥平面BDE;
(3)求:几何体EG-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省烟台市高三统一质量检测考试理科数学试卷(解析版) 题型:解答题
已知函数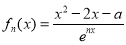 ,其中
,其中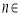 N*,a
N*,a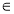 R,e是自然对数的底数.
R,e是自然对数的底数.
(1)求函数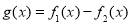 的零点;
的零点;
(2)若对任意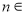 N*,
N*,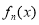 均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
(3)已知k,m N*,k<m,且函数
N*,k<m,且函数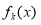 在R上是单调函数,探究函数
在R上是单调函数,探究函数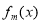 的单调性.
的单调性.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考文科数学试卷(解析版) 题型:解答题
设椭圆E中心在原点,焦点在x轴上,短轴长为4,点Q(2, )在椭圆上.
)在椭圆上.
(1)求椭圆E的方程;
(2)设动直线L交椭圆E于A、B两点,且 ,求△OAB的面积的取值范围.
,求△OAB的面积的取值范围.
(3)过M( )的直线
)的直线 :
: 与过N(
与过N( )的直线
)的直线 :
:
 的交点P(
的交点P( )在椭圆E上,直线MN与椭圆E的两准线分别交于G,H两点,求
)在椭圆E上,直线MN与椭圆E的两准线分别交于G,H两点,求 ·
· 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考文科数学试卷(解析版) 题型:选择题
对于三次函数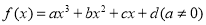 ,给出定义:设
,给出定义:设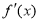 是函数
是函数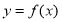 的导数,
的导数,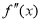 是
是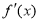 的导数,若方程
的导数,若方程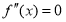 有实数解
有实数解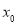 ,则称点
,则称点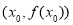 为函数
为函数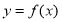 的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数
的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数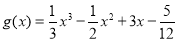 ,则
,则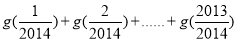 =( )
=( )
A. 2011 B. 2012 C. 2013 D. 2014
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考文科数学试卷(解析版) 题型:选择题
某程序框图如图所示,若该程序运行后输出的值是 ,则( )
,则( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届四川省高三10月月考理科数学试卷(解析版) 题型:解答题
已知向量 。
。
(1)求 的最小正周期和单调减区间;
的最小正周期和单调减区间;
(2)将函数 的图象向右平移
的图象向右平移 个单位,再将所得图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数
个单位,再将所得图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数 的图象,在△ABC中,角A、B、C的对边分别为
的图象,在△ABC中,角A、B、C的对边分别为 ,若
,若 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知数列{an}满足an=2an-1+2n+1(n∈N,n>1),a3=27,数列{bn}满足bn= (an+t).
(an+t).
(1)若数列{bn}为等差数列,求bn;
(2)在(1)的条件下,求数列{an}的前n项和Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com