
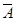 ·
·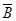 ·
·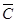 )=P(
)=P(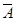 )P(
)P(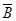 )P(
)P(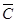 )=0.1×0.2×0.15=0.003,
)=0.1×0.2×0.15=0.003,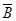 ·
·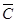 +
+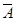 ·B·
·B·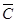 +
+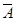 ·
·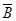 ·C)=P(A)P(
·C)=P(A)P(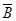 )P(
)P(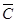 )+P(
)+P(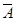 )P(B)P(
)P(B)P(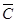 )+P(
)+P(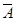 )P(
)P(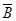 )P(C)=0.056,
)P(C)=0.056,

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源:不详 题型:解答题
 与
与 ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为 。
。 。
。 ,求
,求 的分布列和数学期望。
的分布列和数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:| 运动员编号 |  |  |  |  |  |  |  |  |
| 得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
| 运动员编号 |  |  |  |  |  |  |  |  |
| 得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
| 区间 |  |  |  |
| 人数 | | | |
 内的运动员中随机抽取2人,
内的运动员中随机抽取2人,查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0.432 | B.0.6 | C.0.8 | D.0.288 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 =(m,n),
=(m,n), =(3,6),则向量
=(3,6),则向量 与
与 共线的概率为[
共线的概率为[ 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com