
【题目】已知函数f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若x,y∈[﹣1,1],x+y≠0有(x+y)[f(x)+f(y)]>0.
(1)判断f(x)的单调性,并加以证明;
(2)解不等式 ![]() ;
;
(3)若f(x)≤m2﹣2am+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立.求实数m的取值范围.
【答案】
(1)解:函数f(x)在[﹣1,1]上单调增,证明如下
由题意,设x1,x2∈[﹣1,1],且x1<x2
则x1﹣x2<0
∵x,y∈[﹣1,1],x+y≠0有(x+y)[f(x)+f(y)]>0.
令x=x1,y=﹣x2,
∴f(x1)+f(﹣x2)<0
∵函数f(x)是定义在[﹣1,1]上的奇函数
∴f(x1)﹣f(x2)<0
∴函数f(x)在[﹣1,1]上单调增
(2)解:由(1)知, ![]() ,解得:
,解得: ![]()
(3)解:由于函数f(x)在[﹣1,1]上单调增,
∴函数f(x)在[﹣1,1]上的最大值为f(1)=1
∴f(x)≤m2﹣2am+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立可转化为:0≤m2﹣2am对所有a∈[﹣1,1]恒成立
∴ ![]() ,
,
解得m≥2或m≤﹣2或m=0
【解析】(1)设x1 , x2∈[﹣1,1],且x1<x2 , 则x1﹣x2<0,利用x,y∈[﹣1,1],x+y≠0有(x+y)[f(x)+f(y)]>0,可得f(x1)+f(﹣x2)<0,根据函数f(x)是定义在[﹣1,1]上的奇函数,即可得函数f(x)在[﹣1,1]上单调增;(2)由(1)知, ![]() ,解之即可;(3)先确定函数f(x)在[﹣1,1]上的最大值为f(1)=1,将f(x)≤m2﹣2am+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立转化为:0≤m2﹣2am对所有a∈[﹣1,1]恒成立,从而可求实数m的取值范围.
,解之即可;(3)先确定函数f(x)在[﹣1,1]上的最大值为f(1)=1,将f(x)≤m2﹣2am+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立转化为:0≤m2﹣2am对所有a∈[﹣1,1]恒成立,从而可求实数m的取值范围.
【考点精析】解答此题的关键在于理解奇偶性与单调性的综合的相关知识,掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆C:x2+y2=4和直线l:x=4,M为l上一动点,A1 , A2为圆C与x轴的两个交点,直线MA1 , MA2与圆C的另一个交点分别为P、Q.
(1)若M点的坐标为(4,2),求直线PQ方程;
(2)求证直线PQ过定点,并求出此定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn是等差数列{an}的前n项和,且S6>S7>S5 , 给出下列五个命题:①d<1;②S11>0;③S12<0;④数列{Sn}中的最大项为S11;⑤|a6|>|a7|.其中正确命题有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
为庆祝“2017年中国长春国际马拉松赛”,某单位在庆祝晚会中进行嘉宾现场抽奖活动.抽奖盒中装有大小相同的6个小球,分别印有“长春马拉松”和“美丽长春”两种标志,摇匀后,规定参加者每次从盒中同时抽取两个小球(登记后放回并摇匀),若抽到的两个小球都印有“长春马拉松”即可中奖,并停止抽奖,否则继续,但每位嘉宾最多抽取3次.已知从盒中抽取两个小球不都是“美丽长春”标志的概率为![]() .
.
(Ⅰ)求盒中印有“长春马拉松”标志的小球个数;
(Ⅱ)用η表示某位嘉宾抽奖的次数,求η的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF= ![]() ,给出下列结论:
,给出下列结论:
(1)AC⊥BE;
(2)EF∥平面ABCD;
(3)三棱锥A﹣BEF的体积为定值;
(4)异面直线AE,BF所成的角为定值.
其中错误的结论有( )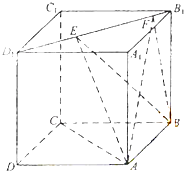
A.0个
B.1 个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知顶点在原点,焦点在x轴上的抛物线被直线y=2x+1截得的弦长为 ![]() .
.
(1)求抛物线的方程;
(2)若抛物线与直线y=2x﹣5无公共点,试在抛物线上求一点,使这点到直线y=2x﹣5的距离最短.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com