
【题目】若点O(0,0)和点 ![]() 分别是双曲线
分别是双曲线 ![]() ﹣y2=1(a>0)的中心和右焦点,A为右顶点,点M为双曲线右支上的任意一点,则
﹣y2=1(a>0)的中心和右焦点,A为右顶点,点M为双曲线右支上的任意一点,则 ![]() 的取值范围为( )
的取值范围为( )
A.[﹣1,+∞)
B.(0,+∞)
C.[﹣2,+∞)
D.[0,+∞)
科目:高中数学 来源: 题型:
【题目】设命题p:方程x2+2mx+1=0有两个不相等的负根,命题q:x∈R,x2+2(m﹣2)x﹣3m+10≥0恒成立.
(1)若命题p、q均为真命题,求m的取值范围;
(2)若命题p∧q为假,命题p∨q为真,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( ) 
A.20
B.22.5
C.22.75
D.25
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对边的边长分别为a,b,c,给出下列四个结论: ①以 ![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
②以 ![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
③以a2 , b2 , c2为边长的三角形一定存在;
④以 ![]() 为边长的三角形一定存在.
为边长的三角形一定存在.
那么,正确结论的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年“五一节”期间,高速公路车辆较多,交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度,采用的方法是:按到达监控点先后顺序,每隔50辆抽取一辆,总共抽取120辆,分别记下其行车速度,将行车速度(km/h)分成七段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),[90,95)后得到如图所示的频率分布直方图,据图解答下列问题: 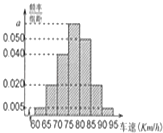
(1)求a的值,并说明交警部门采用的是什么抽样方法?
(2)求这120辆车行驶速度的众数和中位数的估计值(精确到0.1);
(3)若该路段的车速达到或超过90km/h即视为超速行驶,试根据样本估计该路段车辆超速行驶的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设OABC是四面体,G1是△ABC的重心,G是OG1上一点,且OG=3GG1 , 若 ![]() =x
=x ![]() +y
+y ![]() +z
+z ![]() ,则(x,y,z)为( )
,则(x,y,z)为( )
A.( ![]() ,
, ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.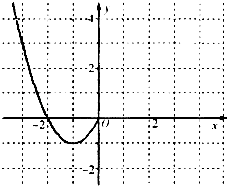
(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间;
(2)写出函数f(x)的解析式和值域;
(3)若方程f(x)﹣m=0有四个解,求m的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com