
【题目】2017年5月27日当今世界围棋排名第一的柯洁在与![]() 的人机大战中中盘弃子认输,至此柯洁与
的人机大战中中盘弃子认输,至此柯洁与![]() 的三场比赛全部结束,柯洁三战全负,这次人机大战再次引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查,根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
的三场比赛全部结束,柯洁三战全负,这次人机大战再次引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查,根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
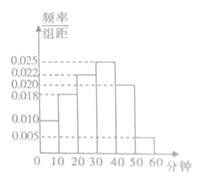
(1)请根据已知条件完成下面![]() 列联表,并据此资料你是否有95%的把握认为“围棋迷”与性别有关?
列联表,并据此资料你是否有95%的把握认为“围棋迷”与性别有关?
非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(2)将上述调查所得到的频率视为概率,现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记被抽取的3名学生中的“围棋迷”人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列,数学期望和方差.
的分布列,数学期望和方差.
独立性检查临界值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | … |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | … |
(参考公式: 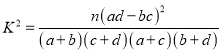 ,其中
,其中![]() )
)
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的两个焦点分别为
的两个焦点分别为![]() ,点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
,点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
(1)求椭圆C的方程;
(2)过点M(1,0)的直线与椭圆C相交于A、B两点,设点N(3,2),记直线AN、BN的斜率分别为k1、k2,求证:k1+k2为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月1日为庆祝中国人民共和国成立70周年在北京天安门广场举行了盛大的阅兵仪式,共有580台(套)装备、160余架各型飞机接受检阅,受阅装备均为中国国产现役主战装备,其中包括部分首次公开亮相的新型装备.例如,在无人作战第三方队中就包括了两型侦察干扰无人机,可以在遥控设备或自备程序控制操纵的情况下执行任务,进行对敌方通讯设施的电磁压制和干扰,甚至压制敌人的防空系统.某作战部门对某处的战场实施“电磁干扰”实验,据测定,该处的“干扰指数”与无人机干扰源的强度和距离之比成正比,比例系数为常数![]() (
(![]() ),现已知相距36
),现已知相距36![]() 的
的![]() 、
、![]() 两处配置两架无人机干扰源,其对敌干扰的强度分别为1和
两处配置两架无人机干扰源,其对敌干扰的强度分别为1和![]() (
(![]() ),它们连线段上任意一点
),它们连线段上任意一点![]() 处的干扰指数
处的干扰指数![]() 等于两机对该处的干扰指数之和,设
等于两机对该处的干扰指数之和,设![]() (
(![]() ).
).
(1)试将![]() 表示为
表示为![]() 的函数,指出其定义域;
的函数,指出其定义域;
(2)当![]() ,
,![]() 时,试确定“干扰指数”最小时
时,试确定“干扰指数”最小时![]() 所处位置.
所处位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设随机变量ξ服从正态分布N(0,1),则下列结论正确的是( )
①P(|ξ|<a)=P(ξ<a)+P(ξ>-a)(a>0);②P(|ξ|<a)=2P(ξ<a)-1(a>0);③P(|ξ|<a)=1-2P(ξ<a)(a>0);④P(|ξ|<a)=1-P(|ξ|≥a)(a>0).
A. ①② B. ②③
C. ①④ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】红外线治疗仪的治疗作用是在红外线照射下,组织温度升高,毛细血管扩张,血流加快,物质代谢增强,组织细胞活力及再生能力提高,对我们身体某些疾病的治疗有着很大的贡献,某药店兼营某种红外线治疗仪,经过近![]() 个月的营销,对销售状况进行相关数据分析,发现月销售量与销售价格有关,其统计数据如下表:
个月的营销,对销售状况进行相关数据分析,发现月销售量与销售价格有关,其统计数据如下表:
每台红外线治疗仪的销售价格: |
|
|
|
|
|
红外线治疗仪的月销售量: |
|
|
|
|
|
(1)根据表中数据求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)①每台红外线治疗仪的价格为![]() 元时,预测红外线治疗仪的月销售量;(四舍五入为整数)
元时,预测红外线治疗仪的月销售量;(四舍五入为整数)
②若该红外线治疗仪的成本为![]() 元/台,药店为使每月获得最大的纯收益,利用(1)中结论,问每台该种红外线治疗仪的销售价格应定为多少元?(四舍五入,精确到
元/台,药店为使每月获得最大的纯收益,利用(1)中结论,问每台该种红外线治疗仪的销售价格应定为多少元?(四舍五入,精确到![]() 元).
元).
参考公式:回归直线方程![]() ,
,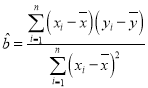 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】历史上,许多人研究过圆锥的截口曲线.如图,在圆锥中,母线与旋转轴夹角为![]() ,现有一截面与圆锥的一条母线垂直,与旋转轴的交点
,现有一截面与圆锥的一条母线垂直,与旋转轴的交点![]() 到圆锥顶点
到圆锥顶点![]() 的距离为
的距离为![]() ,对于所得截口曲线给出如下命题:
,对于所得截口曲线给出如下命题:
①曲线形状为椭圆;
②点![]() 为该曲线上任意两点最长距离的三等分点;
为该曲线上任意两点最长距离的三等分点;
③该曲线上任意两点间的最长距离为![]() ,最短距离为
,最短距离为![]() ;
;
④该曲线的离心率为![]() .其中正确命题的序号为 ( )
.其中正确命题的序号为 ( )
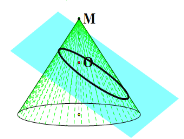
A. ①②④B. ①②③④C. ①②③D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大以来,国家深入推进精准脱贫,加大资金投入,强化社会帮扶,为了更好的服务于人民,派调查组到某农村去考察和指导工作.该地区有200户农民,且都从事水果种植,据了解,平均每户的年收入为3万元.为了调整产业结构,调查组和当地政府决定动员部分农民从事水果加工,据估计,若能动员![]() 户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高
户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高![]() ,而从事水果加工的农民平均每户收入将为
,而从事水果加工的农民平均每户收入将为![]() 万元.
万元.
(1)若动员![]() 户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求
户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,要使这200户农民中从事水果加工的农民的总收入始终不高于从事水果种植的农民的总收入,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人同时参加一次数学测试,共有20道选择题,每题均有4个选项,答对得3分,答错或不答得0分,甲和乙都解答了所有的试题,经比较,他们只有2道题的选项不同,如果甲最终的得分为54分,那么乙的所有可能的得分值组成的集合为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用![]() 列联表,由计算可得
列联表,由计算可得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com