
【题目】如图,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() .过
.过![]() 的平面交
的平面交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
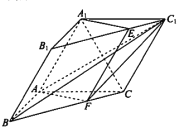
(l)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)记四棱锥![]() 的体积为
的体积为![]() ,三棱柱
,三棱柱![]() 的体积为
的体积为![]() .若
.若![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析;(Ⅲ) ![]() .
.
【解析】试题分析:(l)因为![]() 平面
平面![]() ,由线面垂直的性质可得
,由线面垂直的性质可得![]() ,根据菱形的性质可得
,根据菱形的性质可得![]() ,利用线面垂直的判定定理可得
,利用线面垂直的判定定理可得![]() 平面
平面![]() ;(Ⅱ)由
;(Ⅱ)由![]() ,
, ![]() 平面
平面![]() ,所以
,所以 ![]() 平面
平面![]() ,利用线面平行的性质定理可得
,利用线面平行的性质定理可得![]() ;(Ⅲ) 记三棱锥
;(Ⅲ) 记三棱锥![]() 的体积为
的体积为![]() ,三棱柱
,三棱柱![]() 的体积为
的体积为![]() ,先证明
,先证明![]() ,所以
,所以 ![]() ,结合
,结合![]() , 可得
, 可得 ![]() ,而三棱柱
,而三棱柱![]() 与三棱柱
与三棱柱![]() 等高,由此得
等高,由此得 ![]() .
.
试题解析:(1) 因为 ![]() 平面
平面![]() ,所以
,所以 ![]() .
.
在三棱柱![]() 中,因为
中,因为 ![]() ,所以 四边形
,所以 四边形![]() 为菱形,
为菱形,
所以 ![]() . 所以
. 所以 ![]() 平面
平面![]() .
.
(2)在 三棱柱![]() 中,
中,
因为 ![]() ,
, ![]() 平面
平面![]() ,所以
,所以 ![]() 平面
平面![]() .
.
因为 平面![]() 平面
平面![]() ,所以
,所以 ![]() .
.
(3)记三棱锥![]() 的体积为
的体积为![]() ,三棱柱
,三棱柱![]() 的体积为
的体积为![]() .
.
因为三棱锥![]() 与三棱柱
与三棱柱![]() 同底等高,
同底等高,
所以 ![]() , 所以
, 所以 ![]() .
.
因为 ![]() , 所以
, 所以 ![]() . 因为 三棱柱
. 因为 三棱柱![]() 与三棱柱
与三棱柱![]() 等高,
等高,
所以 △![]() 与△
与△![]() 的面积之比为
的面积之比为![]() , 所以
, 所以 ![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
(1)若平面ABCD⊥平面DCEF,求直线MN与平面DCEF所成角的正弦值;
(2)用反证法证明:直线ME与BN是两条异面直线.
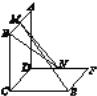
查看答案和解析>>
科目:高中数学 来源: 题型:
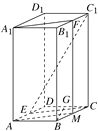
【题目】(2017·泰安模拟)如图,在正四棱柱ABCDA1B1C1D1中,E为AD的中点,F为B1C1的中点.
(1)求证:A1F∥平面ECC1;
(2)在CD上是否存在一点G,使BG⊥平面ECC1?若存在,请确定点G的位置,并证明你的结论,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“中华好诗词”节目的播出,掀起了全民诵读传统诗词经典的热潮.某大学社团为调查大学生对于“中华诗词”的喜好,在该校随机抽取了40名学生,记录他们每天学习“中华诗词”的时间,并整理得到如下频率分布直方图:
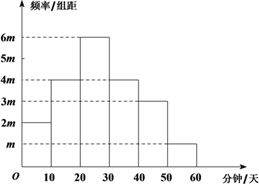
根据学生每天学习“中华诗词”的时间,可以将学生对于“中华诗词”的喜好程度分为三个等级 :
学习时间 (分钟/天) |
|
|
|
等级 | 一般 | 爱好 | 痴迷 |
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ) 从该大学的学生中随机选出一人,试估计其“爱好”中华诗词的概率;
(Ⅲ) 假设同组中的每个数据用该组区间的右端点值代替,试估计样本中40名学生每人每天学习“中华诗词”的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市高中全体学生参加某项测评,按得分评为![]() 两类(评定标准见表1).根据男女学生比例,使用分层抽样的方法随机抽取了10000名学生的得分数据,其中等级为
两类(评定标准见表1).根据男女学生比例,使用分层抽样的方法随机抽取了10000名学生的得分数据,其中等级为![]() 的学生中有40%是男生,等级为
的学生中有40%是男生,等级为![]() 的学生中有一半是女生.等级为
的学生中有一半是女生.等级为![]() 和
和![]() 的学生统称为
的学生统称为![]() 类学生,等级为
类学生,等级为![]() 和
和![]() 的学生统称为
的学生统称为![]() 类学生.整理这10000名学生的得分数据,得到如图2所示的频率分布直方图,
类学生.整理这10000名学生的得分数据,得到如图2所示的频率分布直方图,
类别 | 得分( | |
|
|
|
|
| |
|
|
|
|
| |
表1
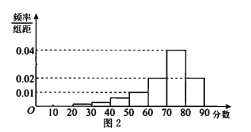
(I)已知该市高中学生共20万人,试估计在该项测评中被评为![]() 类学生的人数;
类学生的人数;
(Ⅱ)某5人得分分别为45,50,55,75,85.从这5人中随机选取2人组成甲组,另外3人组成乙组,求“甲、乙两组各有1名![]() 类学生”的概率;
类学生”的概率;
(Ⅲ)在这10000名学生中,男生占总数的比例为51%, ![]() 类女生占女生总数的比例为
类女生占女生总数的比例为![]() ,
, ![]() 类男生占男生总数的比例为
类男生占男生总数的比例为![]() ,判断
,判断![]() 与
与![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() ,以平面直角坐标系
,以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(1)将曲线![]() 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的![]() 倍、2倍后得到曲线
倍、2倍后得到曲线![]() .试写出直线
.试写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的极坐标方程为:
的极坐标方程为: ![]() .若以极点
.若以极点![]() 为原点,极轴所在直线为
为原点,极轴所在直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(Ⅰ)求圆![]() 的参数方程;
的参数方程;
(Ⅱ)在直角坐标系中,点![]() 是圆
是圆![]() 上动点,试求
上动点,试求![]() 的最大值,并求出此时点
的最大值,并求出此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为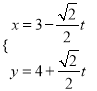 (
(![]() 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,圆
轴正半轴为极轴的极坐标系中,圆![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com