
(1)已知当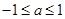 时,不等式
时,不等式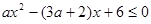 恒成立,求实数
恒成立,求实数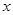 的取值范围
的取值范围
(2)解关于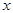 的不等式
的不等式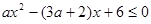 .
.
(1)x=3
(2)当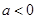 时,解集为:
时,解集为: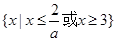 ,当
,当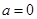 时,解集为:
时,解集为: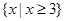
当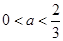 时,解集为:
时,解集为: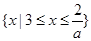 当
当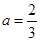 时,解集为:
时,解集为: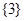 当
当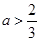 时,解集为:
时,解集为: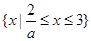
【解析】
试题分析:解:(1)原式可化为: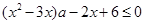 1分
1分
设
则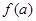 为关于
为关于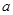 的一次函数,由题意:
的一次函数,由题意:
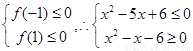 3分
3分
解得: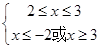 6分
6分
 8分
8分
(2)原不等式可化为: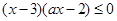 10分
10分
那么由于a=0表示的为一次函数,a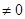 为二次函数,那么分为两大类,结合开口方向和根的大小,和二次函数图形可知,需要整体分为a>0,a=0,a<0来求解,那么对于
为二次函数,那么分为两大类,结合开口方向和根的大小,和二次函数图形可知,需要整体分为a>0,a=0,a<0来求解,那么对于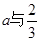 的大小将会影响到根的大小,所以要将a分为
的大小将会影响到根的大小,所以要将a分为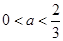 和
和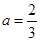 ,以及
,以及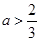 来得到结论,那么可知有
来得到结论,那么可知有
当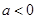 时,原不等式的解集为:
时,原不等式的解集为: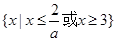 12分
12分
当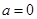 时,原不等式的解集为:
时,原不等式的解集为: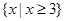 13分
13分
当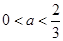 时,原不等式的解集为:
时,原不等式的解集为: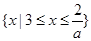 14分
14分
当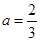 时,原不等式的解集为:
时,原不等式的解集为: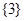 15分
15分
当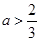 时,原不等式的解集为:
时,原不等式的解集为: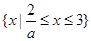 16分
16分
考点:二次不等式的解集
点评:主要是考查了含有参数的一元二次不等式的求解运用,属于中档题。体现了分类讨论思想的运用。


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
设f(x)是定义在区间![]() 上以2为周期的函数,对
上以2为周期的函数,对![]() ,用
,用![]() 表示区间
表示区间![]() 已知当
已知当![]() 时,f(x)=x2.
时,f(x)=x2.
(1)求f(x)在![]() 上的解析表达式;
上的解析表达式;
(2)对自然数k,求集合![]() 不等的实根}
不等的实根}
查看答案和解析>>
科目:高中数学 来源:2012-2013学年天津市高一(上)期末数学试卷(解析版) 题型:解答题
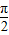 )的图象如图所示.
)的图象如图所示. 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的对称轴方程;
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的对称轴方程;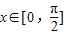 时,方程f(x)=2a-3有两个不等的实根x1,x2,求实数a的取值范围,并求此时x1+x2的值.
时,方程f(x)=2a-3有两个不等的实根x1,x2,求实数a的取值范围,并求此时x1+x2的值.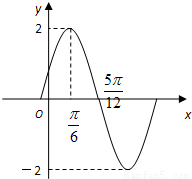
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高三第二次阶段性考试数学试卷(解析版) 题型:解答题
(本题满分14分) 已知 是方程
是方程 的两个不等实根,函数
的两个不等实根,函数 的定义域为
的定义域为 .
.
⑴当 时,求函数
时,求函数 的值域;
的值域;
⑵证明:函数 在其定义域
在其定义域 上是增函数;
上是增函数;
⑶在(1)的条件下,设函数 ,
,
若对任意的 ,总存在
,总存在 ,使得
,使得 成立,
成立,
求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
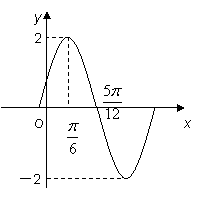
已知函数![]() (其中
(其中![]() )的图象如图所示.
)的图象如图所示.
(1)求![]() 的解析式;
的解析式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再将得到的图象上各点的横坐标伸长到
个单位后,再将得到的图象上各点的横坐标伸长到
原来的![]() 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数![]() 的图象,求
的图象,求![]() 的对称轴方程;
的对称轴方程;
 (3)当
(3)当![]() 时,方程
时,方程![]() 有两个不等的实根
有两个不等的实根![]() ,
,![]() ,求实数
,求实数![]() 的取值范围,
的取值范围,
并求此时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com