
| A. | l∥α | B. | l⊥α | C. | l?α | D. | A、C都有可能 |
分析 直线l的一个方向向量$\overrightarrow a=(2,2,-2)$,平面α的一个法向量为$\overrightarrow b=(1,1,-1)$,可得$\overrightarrow{a}$=2$\overrightarrow{b}$,即可判断出结论.
解答 解:∵直线l的一个方向向量$\overrightarrow a=(2,2,-2)$,
平面α的一个法向量为$\overrightarrow b=(1,1,-1)$,
则$\overrightarrow{a}$=2$\overrightarrow{b}$,∴l⊥α.
故选:B.
点评 本题考查了向量共线定理、线面垂直的判定与性质定理,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 212-57 | B. | 211-47 | C. | 210-38 | D. | 29-30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
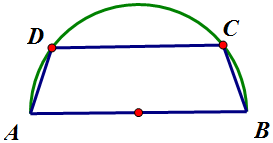 有一块半径为2的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是半圆的直径,上底CD的端点在半圆上.
有一块半径为2的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是半圆的直径,上底CD的端点在半圆上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈[0,2π],sinx≥1 | B. | ¬p:?x∈[-2π,0],sinx>1 | ||
| C. | ¬p:?x∈[0,2π],sinx>1 | D. | ¬p:?x∈[-2π,0],sinx>1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com