
【题目】已知![]() ,函数
,函数![]() .
.
(1)求实数![]() 的值,使得
的值,使得![]() 为奇函数;
为奇函数;
(2)若关于![]() 的方程
的方程![]() 有两个不同实数解,求
有两个不同实数解,求![]() 的取值范围;
的取值范围;
(3)若关于![]() 的不等式
的不等式![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() (3)
(3)![]()
【解析】
(1)若![]() 为奇函数,则
为奇函数,则![]() ,进而可得实数
,进而可得实数![]() 的值,
的值,
(2)若关于![]() 的方程
的方程![]() 有两个不同的实数解,即方程
有两个不同的实数解,即方程 有两个不同实数解,解出两个实数根,然后满足对数的真数为正即可.
有两个不同实数解,解出两个实数根,然后满足对数的真数为正即可.
(3)若关于![]() 的不等式
的不等式![]() 对任意
对任意![]() 恒成立,即
恒成立,即![]() ,对任意
,对任意![]() 恒成立,打开绝对值,进而可得
恒成立,打开绝对值,进而可得![]() 的取值范围.
的取值范围.
(1) ![]() 为奇函数,则
为奇函数,则![]()
即![]()
即![]()
所以![]()
即![]() ,所以
,所以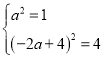
解得:![]()
(2) 方程![]() 有两个不同实数解
有两个不同实数解
即方程![]() 有两个不同实数解
有两个不同实数解
即方程 有两个不同实数解.
有两个不同实数解.
设![]() ,则
,则![]() 可以化为:
可以化为:
![]() ,即
,即![]()
当![]() 时方程不可能有两个不等实数根,所以
时方程不可能有两个不等实数根,所以![]()
则![]() 或
或![]() ,
,
即![]() 或
或![]() ,
,
根据对数的真数必须大于0有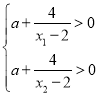 ,即
,即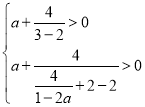
即:![]() 则
则![]() 且
且![]()
又![]() ,则
,则![]()
故方程满足条件的实数![]() 的范围是
的范围是![]() .
.
(3) 不等式![]() 对任意
对任意![]() 恒成立
恒成立
即不等式![]() 对任意
对任意![]() 恒成立.
恒成立.
即![]() 对任意
对任意![]() 恒成立.
恒成立.
所以![]() 对任意
对任意![]() 恒成立.
恒成立.
即![]() 对任意
对任意![]() 恒成立.
恒成立.
即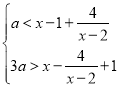 ,
,
由![]()
(当且仅当![]() 时取等号).
时取等号).
![]() 在
在![]() 上单调递增,所以当
上单调递增,所以当![]() 时,
时,![]()
所以![]()
当![]() 时,不等式
时,不等式![]() 对任意
对任意![]() 恒成立.
恒成立.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设![]() ,对于项数为
,对于项数为![]() 的有穷数列
的有穷数列![]() ,令
,令![]() 为
为![]() 中最大值,称数列
中最大值,称数列![]() 为数列
为数列![]() 的“创新数列”.例如数列3,5,4,7的创新数列为3,5,5,7. 考查正整数1,2,…,
的“创新数列”.例如数列3,5,4,7的创新数列为3,5,5,7. 考查正整数1,2,…,![]()
![]() 的所有排列,将每种排列都视为一个有穷数列
的所有排列,将每种排列都视为一个有穷数列![]() .
.
(1)若![]() ,写出创新数列为3,4,4,4的所有数列
,写出创新数列为3,4,4,4的所有数列![]() ;
;
(2)是否存在数列![]() 的创新数列为等比数列?若存在,求出符合条件的
的创新数列为等比数列?若存在,求出符合条件的![]() 的创新数列;若不存在,请说明理由.
的创新数列;若不存在,请说明理由.
(3)是否存在数列![]() ,使它的创新数列为等差数列?若存在,求出满足所有条件的数列
,使它的创新数列为等差数列?若存在,求出满足所有条件的数列![]() 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十九大报告指出,在全面建成小康社会的决胜阶段,让贫困地区同全国人民共同进入全面小康社会是我们党的庄严承诺.在“脱真贫、真脱贫”的过程中,精准扶贫助推社会公平显得尤其重要.若某地区有100户贫困户,经过一年扶贫后,为了考查该地区的“精准扶贫”的成效![]() 该地区脱贫标准为“每户人均年收入不少于4000元”
该地区脱贫标准为“每户人均年收入不少于4000元”![]() ,现从该地区随机抽取A、B两个村庄,再从这两个村庄的贫困户中随机抽取20户,调查每户的现人均年收入,绘制如图所示的茎叶图
,现从该地区随机抽取A、B两个村庄,再从这两个村庄的贫困户中随机抽取20户,调查每户的现人均年收入,绘制如图所示的茎叶图![]() 单位:百元
单位:百元![]() .
.
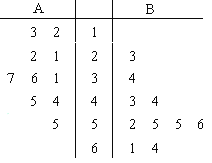
(1)观察茎叶图中的数据,判断哪个村庄扶贫成效较好?并说明理由;
(2)计划对没有脱贫的贫困户进一步实行“精准扶贫”,下一年的资金投入方案如下:对人均年收入不高于2000元的贫困户,每户每年增加扶贫资金5000元;对人均年收入高于2000元但不高于3000元的贫困户,每户每年增加扶贫资金3000元;对人均年收入高于3000元但不高于4000元的贫困户,每户每年增加扶贫资金1000元;对已经脱贫的贫困户不再增加扶贫资金投入.依据此方案,试估计下一年该地区共需要增加扶贫资金多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产的某批产品的销售量![]() 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() (其中
(其中![]() ,
,![]() 为正常数).已知生产该产品还需投入成本
为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为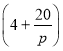 元
元![]() 件.
件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,该公司的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有次水下考古活动中,潜水员需潜入水深为30米的水底进行作业,其用氧量包含以下三个方面:①下潜时,平均速度为每分钟![]() 米,每分钟的用氧量为
米,每分钟的用氧量为![]() 升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟
升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟![]() 米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为
米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为![]() 升;
升;
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,求总用氧量
,求总用氧量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() ),右焦点
),右焦点![]() ,点
,点![]() 在椭圆上;
在椭圆上;
(1)求椭圆C的标准方程;
(2)是否存在过原点的直线l与椭圆C交于A、B两点,且![]() ?若存在,请求出所有符合要求的直线;若不存在,请说明理由.
?若存在,请求出所有符合要求的直线;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为内角
分别为内角![]() ,
,![]() ,
,![]() 的对边,且满
的对边,且满![]() .
.
(1)求![]() 的大小;
的大小;
(2)再在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中,选出两个使
这三个条件中,选出两个使![]() 唯一确定的条件补充在下面的问题中,并解答问题.若________,________,求
唯一确定的条件补充在下面的问题中,并解答问题.若________,________,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() 是各项均为正数的等差数列,其公差
是各项均为正数的等差数列,其公差![]() 大于零.若线段
大于零.若线段![]() ,
,![]() ,
,![]() ,
,![]() 的长分别为
的长分别为![]() ,
,![]() ,
,![]() ,
,![]() ,则( ).
,则( ).
A.对任意的![]() ,均存在以
,均存在以![]() ,
,![]() ,
,![]() 为三边的三角形
为三边的三角形
B.对任意的![]() ,均不存在以
,均不存在以![]() ,
,![]() ,
,![]() 为三边的三角形
为三边的三角形
C.对任意的![]() ,均存在以
,均存在以![]() ,
,![]() ,
,![]() 为三边的三角形
为三边的三角形
D.对任意的![]() ,均不存在以
,均不存在以![]() ,
,![]() ,
,为三边的三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com