
【题目】半圆![]() 的直径的两端点为
的直径的两端点为![]() ,点
,点![]() 在半圆
在半圆![]() 及直径
及直径![]() 上运动,若将点
上运动,若将点![]() 的纵坐标伸长到原来的2倍(横坐标不变)得到点
的纵坐标伸长到原来的2倍(横坐标不变)得到点![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若称封闭曲线上任意两点距离的最大值为该曲线的“直径”,求曲线![]() 的“直径”.
的“直径”.
科目:高中数学 来源: 题型:
【题目】已知直线![]() 、
、![]() 与平面
与平面![]() 、
、![]() 满足
满足![]() ,
,![]() ,
,![]() ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.![]() 是
是![]() 的充分不必要条件
的充分不必要条件
B.![]() 是
是![]() 的充要条件
的充要条件
C.设![]() ,则
,则![]() 是
是![]() 的必要不充分条件
的必要不充分条件
D.设![]() ,则
,则![]() 是
是![]() 的既不充分也不必要条件
的既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司举办捐步公益活动,参与者通过捐赠每天的运动步数获得公司提供的牛奶,再将牛奶捐赠给留守儿童.此活动不但为公益事业作出了较大的贡献,公司还获得了相应的广告效益.据测算,首日参与活动人数为![]() 人,以后每天人数比前一天都增加
人,以后每天人数比前一天都增加![]() ,
,![]() 天后捐步人数稳定在第
天后捐步人数稳定在第![]() 天的水平,假设此项活动的启动资金为
天的水平,假设此项活动的启动资金为![]() 万元,每位捐步者每天可以使公司收益
万元,每位捐步者每天可以使公司收益![]() 元(以下人数精确到
元(以下人数精确到![]() 人,收益精确到
人,收益精确到![]() 元).
元).
(1)求活动开始后第![]() 天的捐步人数,及前
天的捐步人数,及前![]() 天公司的捐步总收益;
天公司的捐步总收益;
(2)活动开始第几天以后公司的捐步总收益可以收回启动资金并有盈余?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 的图像与函数
的图像与函数![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,试用列举法表示集合
,试用列举法表示集合![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区的“微信健步走”活动情况,现用分层抽样的方法从中抽取老、中、青三个年龄段人员进行问卷调查.已知抽取的样本同时满足以下三个条件:
(i)老年人的人数多于中年人的人数;
(ii)中年人的人数多于青年人的人数;
(iii)青年人的人数的两倍多于老年人的人数.
①若青年人的人数为4,则中年人的人数的最大值为___________.
②抽取的总人数的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆
,以原点为圆心,椭圆![]() 的短半轴长为半径的圆与直线
的短半轴长为半径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆方程;
(Ⅱ)设![]() 为椭圆右顶点,过椭圆
为椭圆右顶点,过椭圆![]() 的右焦点的直线
的右焦点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() ),直线
),直线![]() ,
,![]() 分别交直线
分别交直线![]() 于
于![]() ,
,![]() 两点. 求证:
两点. 求证:![]() ,
,![]() 两点的纵坐标之积为定值.
两点的纵坐标之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方体![]() 的棱长为2,E、F、G分别为
的棱长为2,E、F、G分别为![]() 的中点,给出下列命题:
的中点,给出下列命题:
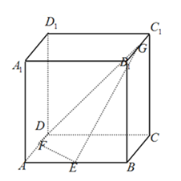
①异面直线EF与AG所成的角的余弦值为![]() ;
;
②过点E、F、G作正方体的截面,所得的截面的面积是![]() ;
;
③![]() 平面
平面![]()
④三棱锥![]() 的体积为1
的体积为1
其中正确的命题是_____________(填写所有正确的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com