
已知3sinα=sin(α+2β),求证:tan(α+β)=2tanβ.
|
思路分析:观察条件等式和结论等式中的角,条件中含有β、2α+β,结论中含有α+β、α,若从条件入手,可采用角的变换,α=(α+β)-β,2α+β=(α+β)+β,展开后转化成齐次整式,约分得出结论. 证明:∵3sinα=3sin[(α+β)-β] =3sin(α+β)cosβ-3cos(α+β)sinβ, sin(α+2β)=sin[(α+β)+β] =sin(α+β)cosβ+cos(α+β)sinβ, 又3sinα=sin(α+2β), ∴3sin(α+β)cosβ-3cos(α+β)sinβ=sin(α+β)cosβ+cos(α+β)sinβ. ∴2sin(α+β)cosβ=4cos(α+β)sinβ. ∴tan(α+β)=2tanβ. 方法归纳:对条件恒等式的证明,若条件复杂,可从化简条件入手得出结论;若结论复杂,可化简结论;若条件和结论都较为复杂,可同时化简它们,直到找到它们间的联系. 深化升华:三角恒等式的证明实质就是由一种结构形式转化为另一种结构形式.因此证明恒等式的基本思路是:证明等式时必须仔细观察等式两边结构上的差异,然后分析这些差异和联系,最后从解决差异入手,施行适当的变换,直至消除这些差异完成恒等式的证明. |


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源:2012人教A版高中数学必修四3.1两角和差的正弦余弦和正切公式(五)(解析版) 题型:选择题
(2010·鞍山一中)已知a=(sinα,1-4cos2α),b=(1,3sinα-2),α∈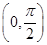 ,若a∥b,则tan
,若a∥b,则tan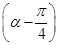 =( )
=( )
A.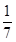 B.-
B.-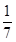 C.
C.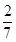 D.-
D.-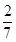
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省高三第三次月考文科数学试卷 题型:解答题
已知向量 =(sin
=(sin ,1),
,1), =(1,cos
=(1,cos ),-
),- .
.
(1) 若 ⊥
⊥ ,求
,求 ;
;
(2) 求| +
+ |的最大值.
|的最大值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三文科数学阶段测试一 题型:填空题
(2010年苏州调研)已知tanx=sin(x+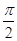 ),则sinx=______________.
),则sinx=______________.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省济宁市高三11月月考文科数学 题型:解答题
(本小题满分12分)
已知向量 =(sin
=(sin ,1),
,1), =(1,cos
=(1,cos ),-
),- .
.
(1) 若 ⊥
⊥ ,求
,求 ;
;
(2) 求| +
+ |的最大值.
|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com