
【题目】设函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若对于任意![]() ,都有
,都有![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】有关部门在某公交站点随机抽取了100名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,乘车等待时间不超过40分钟),将数据按![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() 分组,绘制成如图所示的频率分布直方图.
分组,绘制成如图所示的频率分布直方图.
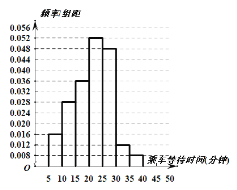
假设乘客乘车等待时间相互独立.
(1)求抽取的100名乘客乘车等待时间的中位数(保留一位小数);
(2)现从该车站等车的乘客中随机抽取4人,记等车时间在![]() 的人数为
的人数为![]() ,用频率估计概率,求随机变量
,用频率估计概率,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,把
,把![]() 上各点横坐标伸长为原来的2倍,纵坐标不变,得到函数
上各点横坐标伸长为原来的2倍,纵坐标不变,得到函数![]() 的图象,关于
的图象,关于![]() 有下述四个结论:
有下述四个结论:
(1)函数![]() 在
在![]() 上是减函数;
上是减函数;
(2)当![]() ,且
,且![]() 时,
时,![]() ,则
,则![]() ;
;
(3)函数![]() (其中
(其中![]() )的最小值为
)的最小值为![]() .
.
其中正确结论的个数为( ).
A.1B.2C.3D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点.
两点.
(1)求过![]() 、
、![]() 、
、![]() 三点的圆
三点的圆![]() 的方程;
的方程;
(2)若![]() 为坐标原点,直线
为坐标原点,直线![]() 与椭圆
与椭圆![]() 和(1)中的圆
和(1)中的圆![]() 分别相切于点
分别相切于点![]() 和点
和点![]() (
(![]() 、
、![]() 不重合),求直线
不重合),求直线![]() 与直线
与直线![]() 的斜率之积.
的斜率之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了推进分级诊疗,实现“基层首诊、双向转诊、急慢分治、上下联动”的诊疗模式,某地区自2016年起全面推行家庭医生签约服务.已知该地区居民约为2000万,从1岁到101岁的居民年龄结构的频率分布直方图如图1所示.为了解各年龄段居民签约家庭医生的情况,现调查了1000名年满18周岁的居民,各年龄段被访者签约率如图2所示.
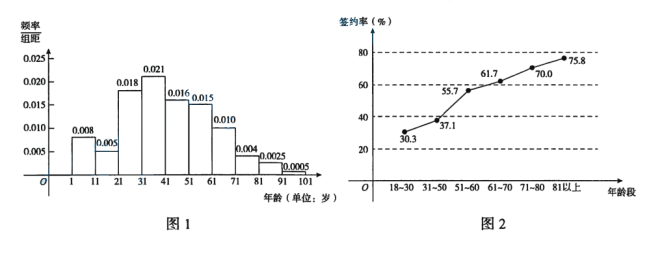
(1)估计该地区年龄在71~80岁且已签约家庭医生的居民人数;
(2)若以图2中年龄在71~80岁居民签约率作为此地区该年龄段每个居民签约家庭医生的概率,则从该地区年龄在71~80岁居民中随机抽取两人,求这两人中恰有1人已签约家庭医生的概率;
(3)据统计,该地区被访者的签约率约为![]() .为把该地区年满18周岁居民的签约率提高到
.为把该地区年满18周岁居民的签约率提高到![]() 以上,应着重提高图2中哪个年龄段的签约率?并结合数据对你的结论作出解释.
以上,应着重提高图2中哪个年龄段的签约率?并结合数据对你的结论作出解释.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“熔喷布”是口罩生产的重要原材料,1吨熔喷布大约可供生产100万只口罩.2020年,制造口罩的企业甲的熔喷布1月份的需求量为100吨,并且从2月份起,每月熔喷布的需求量均比上个月增加10%.企业乙是企业甲熔喷布的唯一供应商,企业乙2020年1月份的产能为100吨,为满足市场需求,从2月份到![]() 月份(
月份(![]() 且
且![]() ),每个月比上个月增加一条月产量为50吨的生产线投入生产,从
),每个月比上个月增加一条月产量为50吨的生产线投入生产,从![]() 月份到9月份不再增加新的生产线.计划截止到9月份,企业乙熔喷布的总产量除供应企业甲的需求外,还剩余不少于990吨的熔喷布可供给其它厂商,则企业乙至少要增加___条熔喷布生产线.
月份到9月份不再增加新的生产线.计划截止到9月份,企业乙熔喷布的总产量除供应企业甲的需求外,还剩余不少于990吨的熔喷布可供给其它厂商,则企业乙至少要增加___条熔喷布生产线.
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】非典和新冠肺炎两场疫情告诉我们:应坚决杜绝食用野生动物,提倡文明健康,绿色环保的生活方式.在我国抗击新冠肺炎期间,某校开展一次有关病毒的网络科普讲座.高三年级男生60人,女生40人参加.按分层抽样的方法,在100名同学中选出5人,则男生中选出________人.再从此5人中选出两名同学作为联络人,则这两名联络人中男女都有的概率是________.(第1空2分,第2空3分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)函数![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(2)曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,是否存在这样的点
,是否存在这样的点![]() 使得直线
使得直线![]() 与曲线
与曲线![]() 也相切,若存在,判断满足条件的点
也相切,若存在,判断满足条件的点![]() 的个数,若不存在,请说明理由.
的个数,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com