
【题目】已知全集U=R,集合A= ![]() ,B={y|y=log2x,4<x<16},
,B={y|y=log2x,4<x<16}, 
(1)求图中阴影部分表示的集合C;
(2)若非空集合D={x|4﹣a<x<a},且D(A∪B),求实数a的取值范围.
科目:高中数学 来源: 题型:
【题目】单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=________;f(n)=________( ) 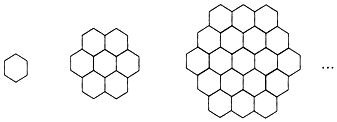
A.37 3n2﹣3n+1
B.38 3n2﹣3n+2
C.36 3n2﹣3n
D.35 3n2﹣3n﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),设
为参数),设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时, ![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)写出![]() 的普遍方程及参数方程;
的普遍方程及参数方程;
(2)以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,设曲线
轴正半轴为极轴建立极坐标系,设曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到
到![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:集合
满足:集合![]() 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数![]() 是等比源函数.
是等比源函数.
(![]() )判断下列函数:①
)判断下列函数:①![]() ;②
;②![]() ;③
;③![]() 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)
(![]() )判断函数
)判断函数![]() 是否为等比源函数,并证明你的结论.
是否为等比源函数,并证明你的结论.
(![]() )证明:
)证明: ![]() ,
, ![]() ,函数
,函数![]() 都是等比源函数.
都是等比源函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法: ①一组数据不可能有两个众数;
②一组数据的方差必为正数,且方差越大,数据的离散程度越大;
③将一组数据中的每个数都加上同一个常数后,方差恒不变;
④在频率分布直方图中,每个长方形的面积等于相应小组的频率.
其中错误的个数有( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如表:
API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若某企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为ω)的关系式为: S= 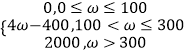 ,试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
,试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关? 附:
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
k2= ![]()
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三某班的一次测试成绩的频率分布表以及频率分布直方图中的部分数据如下,请根据此解答如下问题: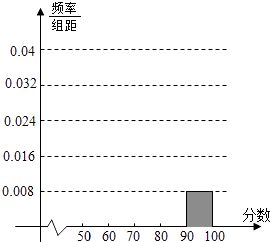
(1)求班级的总人数;
(2)将频率分布表及频率分布直方图的空余位置补充完整;
(3)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100)之间的概率.
分组 | 频数 | 频率 |
[50,60) | 0.08 | |
[60,70) | 7 | |
[70,80) | 10 | |
[80,90) | ||
[90,100) | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2分别是双曲线 ![]() =1(a>0,b>0)的左,右焦点,点F1关于渐近线的对称点恰好在以F2为圆心,|OF2|(O为坐标原点)为半径的圆上,则该双曲线的离心率为 .
=1(a>0,b>0)的左,右焦点,点F1关于渐近线的对称点恰好在以F2为圆心,|OF2|(O为坐标原点)为半径的圆上,则该双曲线的离心率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com