
【题目】已知圆 ![]() ,点
,点 ![]() ,求:
,求:
(1)过点 ![]() 的圆的切线方程;
的圆的切线方程;
(2)![]() 点是坐标原点,连接
点是坐标原点,连接 ![]() ,求
,求 ![]() 的面积
的面积 ![]() .
.
【答案】
(1)解: ![]() .
.
当切线的斜率不存在时,有直线 ![]() 到直线的距离为1,满足条件.
到直线的距离为1,满足条件.
当 ![]() 存在时,设直线方程
存在时,设直线方程 ![]() ,
,
即 ![]() ,解得
,解得 ![]() .
.
∴直线方程为 ![]() 或
或 ![]()
(2)解: ![]() ,
,
![]() ,
,
点 ![]() 到直线
到直线 ![]() 的距离
的距离 ![]() ,
,
![]() .
.
【解析】(1)根据圆x2+y2+Dx+Ey+F=0的圆心坐标为(![]() ,
,![]() ),半径r=
),半径r=![]() 求出已知圆的圆心和半径,当过点A的直线斜率k存在时,根据直线方程的点斜式设出该直线方程,然后根据直线与圆相切时圆心到该直线的距离等于圆的半径r列出方程即可求出斜率k;当过点A的直线斜率不存在时,写出该直线方程,并验证该直线是否与圆C相切;(2)根据两点间距离公式求出
求出已知圆的圆心和半径,当过点A的直线斜率k存在时,根据直线方程的点斜式设出该直线方程,然后根据直线与圆相切时圆心到该直线的距离等于圆的半径r列出方程即可求出斜率k;当过点A的直线斜率不存在时,写出该直线方程,并验证该直线是否与圆C相切;(2)根据两点间距离公式求出![]() ,并根据直线方程的两点式写出直线OA的方程,再根据点到线的距离公式求出点C到直线OA的距离d,那么S=
,并根据直线方程的两点式写出直线OA的方程,再根据点到线的距离公式求出点C到直线OA的距离d,那么S=![]()
![]() d.
d.
【考点精析】解答此题的关键在于理解直线与圆的三种位置关系的相关知识,掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
【题目】下列各小题中,p是q的充分不必要条件的是( ) ①p:m<﹣2或m>6,q:y=x2+mx+m+3有两个零点;
② ![]() ,q:y=f(x)是偶函数;
,q:y=f(x)是偶函数;
③p:cosα=cosβ,q:tanα=tanβ;
④p:A∩B=A,q:(UB)(UA)
A.①②
B.②③
C.③④
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程是 ![]() (t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2+12ρcosθ+11=0. (Ⅰ)说明C是哪种曲线?并将C的方程化为直角坐标方程;
(t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2+12ρcosθ+11=0. (Ⅰ)说明C是哪种曲线?并将C的方程化为直角坐标方程;
(Ⅱ)直线l与C交于A,B两点,|AB|= ![]() ,求l的斜率.
,求l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=4,点E、F分别为AB和PD的中点. 
(1)求证:直线AF∥平面PEC;
(2)求平面PAD与平面PEC所成锐二面角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 在
在 ![]() 上有最大值1和最小值0,设
上有最大值1和最小值0,设 ![]() .
.
(1)求 ![]() 的值;
的值;
(2)若不等式 ![]() 在
在 ![]() 上有解,求实数
上有解,求实数 ![]() 的取值范围;
的取值范围;
(3)若方程 ![]() (
( ![]() 为自然对数的底数)有三个不同的实数解,求实数
为自然对数的底数)有三个不同的实数解,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为响应国家节能减排建设的号召,唤起人们从自己身边的小事做起,开展了以“再小的力量也是一种支持”为主题的宣传教育活动,其中有两则公益广告: ①80部手机,一年就会增加一吨二氧化氮的排放.
②人们在享受汽车带了的便捷舒适的同时,却不得不呼吸汽车排放的尾气.
活动组织者为了解是市民对这两则广告的宣传效果,随机对10﹣60岁的人群抽查了n人,并就两个问题对选取的市民进行提问,其抽样人数频率分布直方图如图所示,宣传效果调查结果如表所示.
宣传效果调查表
广告一 | 广告二 | |||
回答正 | 占本组 | 回答正 | 占本组 | |
[10,20) | 90 | 0.5 | 45 | a |
[20,30) | 225 | 0.75 | k | 0.8 |
[30,40) | b | 0.9 | 252 | 0.6 |
[40,50) | 160 | c | 120 | d |
[50,60] | 10 | e | f | g |
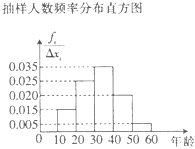
(1)分别写出n,a,b,c,d的值.
(2)若将表中的频率近似看作各年龄组正确回答广告内容的概率,规定正确回答广告一的内容得30元,广告二的内容得60元.组织者随机请一家庭的两成员(大人45岁,孩子17岁),指定大人回答广告一的内容,孩子回答广告二的内容,求该家庭获得奖金数ξ的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,面积为 ![]() 的△ACB是等腰直角三角形且∠ACB=90°,C1B⊥面ABC,C1B=3.
的△ACB是等腰直角三角形且∠ACB=90°,C1B⊥面ABC,C1B=3. 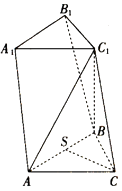
(1)若AB的中点为S,证明:CS⊥C1A.
(2)设 ![]() ,是否存在实数λ,使得直线TB与平面ACC1A1的夹角为
,是否存在实数λ,使得直线TB与平面ACC1A1的夹角为 ![]() ?若存在,求出λ的值;若不存在,请说明理由.
?若存在,求出λ的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com