
【题目】已知抛物线![]() 上的点
上的点![]() 到焦点的距离为
到焦点的距离为![]() .
.

(1)求![]() 的值;
的值;
(2)如上图,已知动线段![]() (
(![]() 在
在![]() 的右边)在直线
的右边)在直线![]() 上,且
上,且![]() ,现过
,现过![]() 作
作![]() 的切线,取左边的切点
的切线,取左边的切点![]() ,过
,过![]() 作
作![]() 的切线,取右边的切点为
的切线,取右边的切点为![]() ,当
,当![]() ,求
,求![]() 点的横坐标
点的横坐标![]() 的值.
的值.
 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:
【题目】某次知识竞赛规则如下:在主办方预设的7个问题中,选手若能连续正确回答出两个问题,即停止答题,晋级下一轮.假设某选手正确回答每个问题的概率都是0.7,且每个问题的回答结果相互独立,则该选手恰好回答了5个问题就晋级下一轮的概率等于( )
A.0.07497B.0.92503C.0.1323D.0.6174
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0),F1,F2为椭圆的左右焦点,过F2的直线交椭圆与A、B两点,∠AF1B=90°,2
1(a>b>0),F1,F2为椭圆的左右焦点,过F2的直线交椭圆与A、B两点,∠AF1B=90°,2![]() ,则椭圆的离心率为( )
,则椭圆的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩形ABCD中,![]() ,
,![]() ,沿矩形对角线BD将
,沿矩形对角线BD将![]() 折起形成四面体ABCD,在这个过程中,现在下面四个结论:①在四面体ABCD中,当
折起形成四面体ABCD,在这个过程中,现在下面四个结论:①在四面体ABCD中,当![]() 时,
时,![]() ;②四面体ABCD的体积的最大值为
;②四面体ABCD的体积的最大值为![]() ;③在四面体ABCD中,BC与平面ABD所成角可能为
;③在四面体ABCD中,BC与平面ABD所成角可能为![]() ;④四面体ABCD的外接球的体积为定值.其中所有正确结论的编号为( )
;④四面体ABCD的外接球的体积为定值.其中所有正确结论的编号为( )
A.①④B.①②C.①②④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() 为坐标原点,
为坐标原点, ![]() 是双曲线上在第一象限内的点,直线
是双曲线上在第一象限内的点,直线![]() 分别交双曲线
分别交双曲线![]() 左、右支于另一点
左、右支于另一点![]() ,
, ![]() ,且
,且![]() ,则双曲线
,则双曲线![]() 的离心率为( )
的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第24届冬奥会将于2022年2月4日至2月22日在北京市和河北省张家口市联合举行,这是中国历史上第一次举办冬季奥运会.为了宣传冬奥会,让更多的人了解、喜爱冰雪项目,某校高三年级举办了冬奥会知识竞赛(总分100分),并随机抽取了![]() 名中学生的成绩,绘制成如图所示的频率分布直方图.已知前三组的频率成等差数列,第一组和第五组的频率相同.
名中学生的成绩,绘制成如图所示的频率分布直方图.已知前三组的频率成等差数列,第一组和第五组的频率相同.
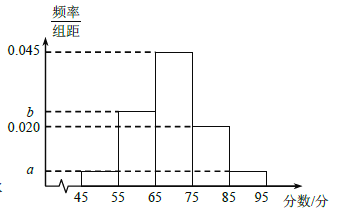
(Ⅰ)求实数![]() ,
,![]() 的值,并估计这
的值,并估计这![]() 名中学生的成绩平均值
名中学生的成绩平均值![]() ;(同一组中的数据用该组区间的中点值作代表)
;(同一组中的数据用该组区间的中点值作代表)
(Ⅱ)已知抽取的![]() 名中学生中,男女生人数相等,男生喜欢花样滑冰的人数占男生人数的
名中学生中,男女生人数相等,男生喜欢花样滑冰的人数占男生人数的![]() ,女生喜欢花样滑冰项的人数占女生人数的
,女生喜欢花样滑冰项的人数占女生人数的![]() ,且有95%的把握认为中学生喜欢花样滑冰与性别有关,求
,且有95%的把握认为中学生喜欢花样滑冰与性别有关,求![]() 的最小值.
的最小值.
参考数据及公式如下:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
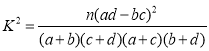 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com