
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:
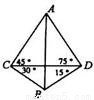
 我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知DC=6000米,∠ACD=45°,∠ADC=75°,目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图所示).求炮兵阵地到目标的距离(结果保留根号).
我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知DC=6000米,∠ACD=45°,∠ADC=75°,目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图所示).求炮兵阵地到目标的距离(结果保留根号).查看答案和解析>>
科目:高中数学 来源: 题型:
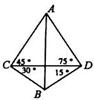
 如图所示,我炮兵阵地位于地面A处,两观察所分别位于地面C处和D处,已知CD=6000 m,∠ACD=45°,∠ADC=75°,目标出现于地面B处时测得∠BCD=30°,∠BDC=15°,则炮兵阵地到目标的距离是
如图所示,我炮兵阵地位于地面A处,两观察所分别位于地面C处和D处,已知CD=6000 m,∠ACD=45°,∠ADC=75°,目标出现于地面B处时测得∠BCD=30°,∠BDC=15°,则炮兵阵地到目标的距离是查看答案和解析>>
科目:高中数学 来源: 题型:
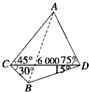
我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知CD=6000m ,
∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°∠BDC=15°(如图)求:炮兵阵地到目标的距离.
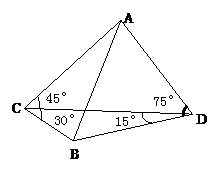
查看答案和解析>>
科目:高中数学 来源:2014届福建龙岩一中高二上学期第一学段考试理科数学试卷(解析版) 题型:解答题
(本题满分13分)我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知CD=6 ,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.
,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.

查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省龙岩一中高二(上)第一学段(模块)考试数学试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com