
已知向量
 函数
函数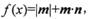 且最小正周期为
且最小正周期为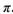 .
.
(I)求函数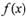 的最大值,并写出相应的X的取值集合;
的最大值,并写出相应的X的取值集合;
(II)在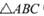 中,角A,B, C所对的边分别为a, b,c,且
中,角A,B, C所对的边分别为a, b,c,且 ,c=3,
,c=3,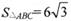 ,求b的值.
,求b的值.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
| ||
| sinx+cosx |
| π |
| 4 |
| a |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2006-2007学年上学期豫北地区高三四校数学联考试题(附答案) 题型:044
已知向量![]() ,ω>0,记函数f(x)==
,ω>0,记函数f(x)==![]() ,已知f(x)的最小正周期为
,已知f(x)的最小正周期为![]() .
.
(1)求ω的值;
(2)设△ABC的三边a,b,c满足b2=ac,且边b所对的角为x,求此时函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省绵阳市高三第二次月考文科数学试卷 题型:解答题
已知向量
 ,函数
,函数 —且最小正周斯为
—且最小正周斯为 ,
,
(1) 求函数, 的最犬值,并写出相应的x的取值集合;
的最犬值,并写出相应的x的取值集合;
(2)在 中角A,B,C所对的边分别为a,b,c且
中角A,B,C所对的边分别为a,b,c且 ,求b的值.
,求b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com