
【题目】如图,在平面直角坐标系xOy中,椭圆![]() 的右焦点、右顶点分别为F,A,过原点的直线与椭圆C交于点P、Q(点P在第一象限内),连结PA,QF.若
的右焦点、右顶点分别为F,A,过原点的直线与椭圆C交于点P、Q(点P在第一象限内),连结PA,QF.若![]() ,
,![]() 的面积是
的面积是![]() 面积的3倍.
面积的3倍.
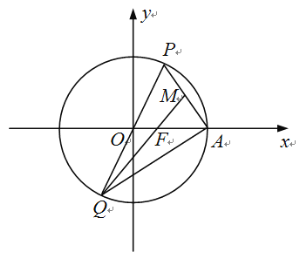
(1)求椭圆C的标准方程;
(2)已知M为线段PA的中点,连结QA,QM.
①求证:Q,F,M三点共线;
②记直线QP,QM,QA的斜率分别为![]() ,
,![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的面积.
的面积.
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】某市在开展创建“全国文明城市”活动中,工作有序扎实,成效显著,尤其是城市环境卫生大为改观,深得市民好评.“创文”过程中,某网站推出了关于环境治理和保护问题情况的问卷调查,现从参与问卷调查的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
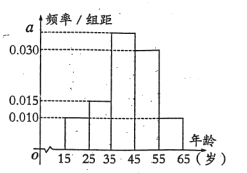
(1)求出a的值;
(2)若已从年龄较小的第1,2组中用分层抽样的方法抽取5人,现要再从这5人中随机抽取3人进行问卷调查,设第2组抽到![]() 人,求随机变量
人,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体A-BCD中,已知平面![]() 平面BCD,
平面BCD,![]() 为正三角形,
为正三角形,![]() 为等腰直角三角形,其中C为直角顶点,E,F分别为校AC,AD的中点.
为等腰直角三角形,其中C为直角顶点,E,F分别为校AC,AD的中点.
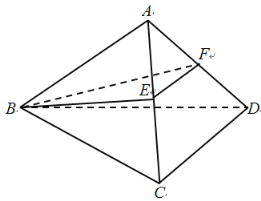
(1)求证:![]() 平面BEF;
平面BEF;
(2)求证:![]() 平面ACD.
平面ACD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在传染病学中,通常把从致病刺激物侵人机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期. 一研究团队统计了某地区1000名患者的相关信息,得到如下表格:
潜伏期(单位:天) |
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
(1)求这1000名患者的潜伏期的样本平均数x (同一组中的数据用该组区间的中点值作代表) ;
(2)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表.请将列联表补充完整,并根据列联表判断是否有95%的把握认为潜伏期与患者年龄有关;
潜伏期 | 潜伏期 | 总计 | |
|
| ||
|
| ||
总计 |
|
(3)以这1000名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立,为了深入研究,该研究团队随机调查了20名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
附:
|
|
|
|
|
|
|
|
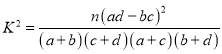 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD是正方形,AE⊥平面ABCD,PD∥AE,PD=AD=2EA=2,G,F,H分别为BE,BP,PC的中点.
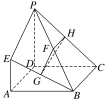
(1)求证:平面ABE⊥平面GHF;
(2)求直线GH与平面PBC所成的角θ的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学在假期进行社会实践活动,对![]() 岁的人群随机抽取n人进行了一次当前投资生活方式——“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
岁的人群随机抽取n人进行了一次当前投资生活方式——“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
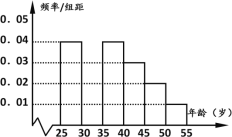
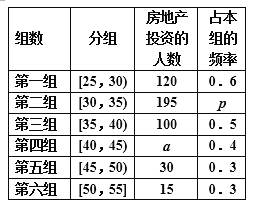
(Ⅰ)求![]() ,
,![]() ,
,![]() 的值;
的值;
(Ⅱ)从年龄在![]() 岁的“房地产投资”人群中采取分层抽样法抽取9人参加投资管理学习活动,其中选取3人作为代表发言,记选取的3名代表中年龄在
岁的“房地产投资”人群中采取分层抽样法抽取9人参加投资管理学习活动,其中选取3人作为代表发言,记选取的3名代表中年龄在![]() 岁的人数为
岁的人数为![]() ,求
,求![]() 的分布列和期望
的分布列和期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面PAD,E是
平面PAD,E是![]() 的中点,F是DC上一点,G是PC上一点,且
的中点,F是DC上一点,G是PC上一点,且![]() ,
,![]() .
.
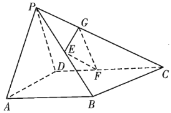
(1)求证:平面![]() 平面PAB;
平面PAB;
(2)若![]() ,
,![]() ,求直线PB与平面ABCD所成角的正弦值.
,求直线PB与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某项针对我国《义务教育数学课程标准》的研究中,列出各个学段每个主题所包含的条目数(如下表),下图是统计表的条目数转化为百分比,按各学段绘制的等高条形图,由图表分析得出以下四个结论,其中错误的是( )
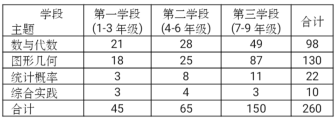
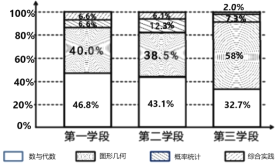
A.除了“综合实践”外,其它三个领域的条目数都随着学段的升高而增加,尤其“图象几何” 在第三学段增加较多,约是第二学段的![]() 倍.
倍.
B.所有主题中,三个学段的总和“图形几何”条目数最多,占50%,综合实践最少,约占4% .
C.第一、二学段“数与代数”条目数最多,第三学段“图形几何”条目数最多.
D.“数与代数”条目数虽然随着学段的增长而增长,而其百分比却一直在减少.“图形几何”条目数,百分比都随学段的增长而增长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com