
ЁОЬтФПЁПНќФъРДЮвЙњЕчзгЩЬЮёаавЕгРДЗЂеЙЕФаТЛњгіЃЌгыДЫЭЌЪБЃЌЯрЙиЙмРэВПУХЭЦГіСЫеыЖдЕчЩЬЩЬЦЗКЭЗўЮёЕФЦРМлЬхЯЕЃЎЯжДгЦРМлЯЕЭГжабЁГі200ДЮГЩЙІНЛвзЃЌВЂЖдЦфЦРМлНјааЭГМЦЃЌЖдЩЬЦЗКУЦРТЪЮЊ![]() ЃЌЖдЗўЮёКУЦРТЪЮЊ
ЃЌЖдЗўЮёКУЦРТЪЮЊ![]() ЃЌЦфжаЖдЩЬЦЗКЭЗўЮёЖМзіГіКУЦРЕФНЛвзЮЊ80ДЮЃЎ
ЃЌЦфжаЖдЩЬЦЗКЭЗўЮёЖМзіГіКУЦРЕФНЛвзЮЊ80ДЮЃЎ
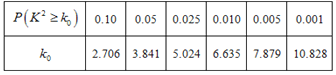
ЃЈ1ЃЉЪЧЗёПЩвддкЗИДэЮѓТЪВЛГЌЙ§0.1%ЕФЧАЬсЯТЃЌШЯЮЊЩЬЦЗКУЦРгыЗўЮёКУЦРгаЙиЃП
ЃЈ2ЃЉШєеыЖдЩЬЦЗЕФКУЦРТЪЃЌВЩгУЗжВуГщбљЕФЗНЪНДгет200ДЮНЛвзжаШЁГі5ДЮНЛвзЃЌВЂДгжабЁдёСНДЮНЛвзНјааПЭЛЇЛиЗУЃЌЧѓжЛгавЛДЮКУЦРЕФИХТЪЃЎ
зЂЃК1.
зЂ2. 
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉ![]() .
.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩвбжЊСаГіЙигкЩЬЦЗКЭЗўЮёЦРМлЕФ2ЁС2СаСЊБэЃЌДњШыЙЋЪНЧѓЕУk2ЕФжЕЃЌЖдгІЪ§БэЕУД№АИЃЛ
ЃЈ2ЃЉВЩгУЗжВуГщбљЕФЗНЪНДгет200ДЮНЛвзжаШЁГі5ДЮНЛвзЃЌдђКУЦРЕФНЛвзДЮЪ§ЮЊ3ДЮЃЌВЛТњвтЕФДЮЪ§ЮЊ2ДЮЃЌРћгУУЖОйЗЈЕУЕНДг5ДЮНЛвзжаЃЌШЁГі2ДЮЕФЫљгаШЁЗЈЃЌВщГіЦфжажЛгавЛДЮКУЦРЕФЧщПіЪ§ЃЌШЛКѓРћгУЙХЕфИХаЭИХТЪМЦЫуЙЋЪНЧѓЕУжЛгавЛДЮКУЦРЕФИХТЪЃЎ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉгЩЬтвтПЩЕУЙигкЩЬЦЗЦРМлКЭЗўЮёЦРМлЕФ![]() СаСЊБэЃК
СаСЊБэЃК
ЖдЗўЮёКУЦР | ЖдЗўЮёВЛТњвт | КЯМЦ | |
ЖдЩЬЦЗКУЦР | 80 | 40 | 120 |
ЖдЩЬЦЗВЛТњвт | 70 | 10 | 80 |
КЯМЦ | 150 | 50 | 200 |
Ыљвд![]() ЃЌ
ЃЌ
ЫљвдПЩвддкЗИДэЮѓИХТЪВЛГЌЙ§0.1%ЕФЧАЬсЯТЃЌШЯЮЊЩЬЦЗКУЦРгыЗўЮёКУЦРгаЙиЃЎ
ЃЈ2ЃЉШєеыЖдЩЬЦЗЕФКУЦРТЪЃЌВЩгУЗжВуГщбљЕФЗНЪНДгет200ДЮНЛвзжаШЁГі5ДЮНЛвзЃЌдђКУЦРЕФНЛвзДЮЪ§ЮЊ3ДЮЃЌВЛТњвтЕФДЮЪ§ЮЊ2ДЮЃЌСюКУЦРЕФНЛвзЮЊ![]() ЃЌВЛТњвтЕФНЛвзЮЊ
ЃЌВЛТњвтЕФНЛвзЮЊ![]() .
.
Дг5ДЮНЛвзжаЃЌШЁГі2ДЮЕФЫљгаШЁЗЈ![]() ЃЎЙВМЦ10жжЧщПіЃЎ
ЃЎЙВМЦ10жжЧщПіЃЎ
ЦфжажЛгавЛДЮКУЦРЕФЧщПіЪЧ![]() ЃЌЙВМЦ6жжЧщПіЃЎ
ЃЌЙВМЦ6жжЧщПіЃЎ
вђДЫЃЌжЛгавЛДЮКУЦРЕФИХТЪЮЊ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊAЃЌBЃЌCЮЊШёНЧЁїABCЕФФкНЧЃЌ ![]() =ЃЈsinAЃЌsinBsinCЃЉЃЌ
=ЃЈsinAЃЌsinBsinCЃЉЃЌ ![]() =ЃЈ1ЃЌЉ2ЃЉЃЌ
=ЃЈ1ЃЌЉ2ЃЉЃЌ ![]() ЁЭ
ЁЭ ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉtanBЃЌtanBtanCЃЌtanCФмЗёЙЙГЩЕШВюЪ§СаЃПВЂжЄУїФуЕФНсТлЃЛ
ЃЈ2ЃЉЧѓtanAtanBtanCЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
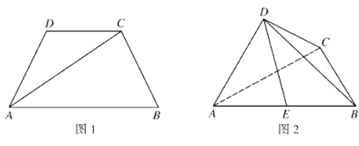
ЁОЬтФПЁПдквЛДЮЙКЮяГщНБЛюЖЏжаЃЌМйЩшФГ10еХШЏжагавЛЕШНБШЏ1еХЃЌПЩЛёМлжЕ50дЊЕФНБЦЗЃЛгаЖўЕШНБШЏ3еХЃЌУПеХПЩЛёМлжЕ10дЊЕФНБЦЗЃЛЦфгр6еХУЛгаНБЃЌФГЙЫПЭДгДЫ10еХШЏжаШЮГщ2еХЃЌЧѓЃК
ЃЈЂёЃЉИУЙЫПЭжаНБЕФИХТЪЃЛ
ЃЈЂђЃЉИУЙЫПЭЛёЕУЕФНБЦЗзмМлжЕІЮЃЈдЊЃЉЕФИХТЪЗжВМСаКЭЦкЭћEІЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ![]() ,ЫФБпаЮ
,ЫФБпаЮ![]() ЮЊЕШбќЬнаЮ,
ЮЊЕШбќЬнаЮ, ![]() ,НЋ
,НЋ![]() би
би![]() елЦ№,ЪЙЕУЦНУц
елЦ№,ЪЙЕУЦНУц![]() ЦНУц
ЦНУц![]() ЮЊ
ЮЊ![]() ЕФжаЕу,СЌНг
ЕФжаЕу,СЌНг![]() (ШчЭМ2).
(ШчЭМ2).
(1)ЧѓжЄ: ![]() ;
;
(2)ЧѓжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩЕФНЧЕФе§ЯвжЕ.
ЫљГЩЕФНЧЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩш![]() ЃЌгж
ЃЌгж![]() ЪЧвЛИіГЃЪ§ЃЌвбжЊ
ЪЧвЛИіГЃЪ§ЃЌвбжЊ![]() Лђ
Лђ![]() ЪБЃЌ
ЪБЃЌ ![]() жЛгавЛИіЪЕИљЃЌЕБ
жЛгавЛИіЪЕИљЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() гаШ§ИіЯрвьЪЕИљЃЌИјГіЯТСаУќЬтЃК
гаШ§ИіЯрвьЪЕИљЃЌИјГіЯТСаУќЬтЃК
Ђй![]() КЭ
КЭ![]() гавЛИіЯрЭЌЕФЪЕИљЃЛ
гавЛИіЯрЭЌЕФЪЕИљЃЛ
Ђк![]() КЭ
КЭ![]() гавЛИіЯрЭЌЕФЪЕИљЃЛ
гавЛИіЯрЭЌЕФЪЕИљЃЛ
Ђл![]() ЕФШЮвЛЪЕИљДѓгк
ЕФШЮвЛЪЕИљДѓгк![]() ЕФШЮвЛЪЕИљЃЛ
ЕФШЮвЛЪЕИљЃЛ
Ђм![]() ЕФШЮвЛЪЕИљаЁгк
ЕФШЮвЛЪЕИљаЁгк![]() ЕФШЮвЛЪЕИљЃЎ
ЕФШЮвЛЪЕИљЃЎ
Цфжае§ШЗУќЬтЕФИіЪ§ЮЊЃЈ ЃЉ
A. 3 B. 2 C. 1 D. 0
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}Тњзуa1=1ЃЌan+1+an= ![]() Љ
Љ ![]() ЃЌnЁЪN* ЃЎ
ЃЌnЁЪN* ЃЎ
ЃЈЂёЃЉЧѓa2 ЃЌ a3 ЃЌ a4ЃЛ
ЃЈЂђЃЉВТЯыЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЌВЂгУЪ§бЇЙщФЩЗЈжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4-4ЃКзјБъЯЕгыВЮЪ§ЗНГЬ
дкжБНЧзјБъЯЕ![]() жаЃЌвд
жаЃЌвд![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌдВ
жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌдВ![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ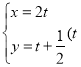 ЮЊВЮЪ§ЃЉЃЌжБЯп
ЮЊВЮЪ§ЃЉЃЌжБЯп![]() КЭдВ
КЭдВ![]() НЛгк
НЛгк![]() СНЕуЃЌ
СНЕуЃЌ![]() ЪЧдВ
ЪЧдВ![]() ЩЯВЛЭЌгк
ЩЯВЛЭЌгк![]() ЕФШЮвтвЛЕуЃЎ
ЕФШЮвтвЛЕуЃЎ
ЃЈ1ЃЉЧѓдВаФЕФМЋзјБъЃЛ
ЃЈ2ЃЉЧѓЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыЕФзюДѓжЕЃЎ
ЕФОрРыЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвдЦНУцжБНЧзјБъЯЕ![]() ЕФдЕуЮЊМЋЕуЃЌ
ЕФдЕуЮЊМЋЕуЃЌ ![]() жсе§АыжсЮЊМЋжсЧвШЁЯрЭЌЕФЕЅЮЛГЄЖШНЈСЂМЋзјБъЯЕЃЎвбжЊЕу
жсе§АыжсЮЊМЋжсЧвШЁЯрЭЌЕФЕЅЮЛГЄЖШНЈСЂМЋзјБъЯЕЃЎвбжЊЕу![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ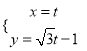 ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌЕу
ЮЊВЮЪ§ЃЉЃЌЕу![]() дкЧњЯп
дкЧњЯп![]() ЩЯЃЎ
ЩЯЃЎ
ЃЈ1ЃЉЧѓдкЦНУцжБНЧзјБъЯЕ![]() жаЕу
жаЕу![]() ЕФЙьМЃЗНГЬКЭЧњЯп
ЕФЙьМЃЗНГЬКЭЧњЯп![]() ЕФЦеЭЈЗНГЬЃЛ
ЕФЦеЭЈЗНГЬЃЛ
ЃЈ2ЃЉЧѓ![]() ЕФзюДѓжЕЃЎ
ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§fЃЈxЃЉ=lnxЉax+ ![]() Љ1ЃЎ ЃЈЂёЃЉЕБa=1ЪБЃЌЧѓЧњЯпfЃЈxЃЉдкx=1ДІЕФЧаЯпЗНГЬЃЛ
Љ1ЃЎ ЃЈЂёЃЉЕБa=1ЪБЃЌЧѓЧњЯпfЃЈxЃЉдкx=1ДІЕФЧаЯпЗНГЬЃЛ
ЃЈЂђЃЉЕБa= ![]() ЪБЃЌЧѓКЏЪ§fЃЈxЃЉЕФЕЅЕїЧјМфЃЛ
ЪБЃЌЧѓКЏЪ§fЃЈxЃЉЕФЕЅЕїЧјМфЃЛ
ЃЈЂѓЃЉдкЃЈЂђЃЉЕФЬѕМўЯТЃЌЩшКЏЪ§gЃЈxЃЉ=x2Љ2bxЉ ![]() ЃЌШєЖдгкx1ЁЪ[1ЃЌ2]ЃЌx2ЁЪ[0ЃЌ1]ЃЌЪЙfЃЈx1ЃЉЁнgЃЈx2ЃЉГЩСЂЃЌЧѓЪЕЪ§bЕФШЁжЕЗЖЮЇЃЎ
ЃЌШєЖдгкx1ЁЪ[1ЃЌ2]ЃЌx2ЁЪ[0ЃЌ1]ЃЌЪЙfЃЈx1ЃЉЁнgЃЈx2ЃЉГЩСЂЃЌЧѓЪЕЪ§bЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com