【题目】天津市某高中团委在2019年12月4日开展了以“学法、遵法、守法”为主题的学习活动．为检查该学校组织学生学习的效果，现从该校高一、高二、高三的学生中分别选取了4人，3人，3人作为代表进行问卷测试．具体要求：每位学生要从10个有关法律、法规的问题中随机抽出4个问题进行作答．
（1）若从这10名学生中任选3人，求这3名学生分别来自三个年级的概率；
（2）若这10人中的某学生能答对10道题中的7道题，另外3道题回答不对，记
表示该名学生答对问题的个数，求随机变量的分布列及数学期望．
科目：高中数学 来源： 题型：
【题目】为了解共享单车在
市的使用情况，某调查机构借助网络进行了问卷调查，并从参与调查的网友中随机抽取了
人进行分析，得到如下列联表（单位：人）.
经常使用 | 偶尔使用或不使用 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
（1）根据以上数据，能否在犯错误的概率不超过
的前提下认为市使用共享单车的情况与年龄有关；
（2）（i）现从所选取的
岁以上的网友中，采用分层抽样的方法选取
人，再从这人中随机选出
人赠送优惠券，求选出的人中至少有
人经常使用共享单车的概率；
（ii）将频率视为概率，从市所有参与调查的网友中随机选取人赠送礼品，记其中经常使用共享单车的人数为
，求的数学期望和方差.
参考公式：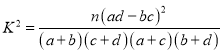
，其中
.
参考数据：
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设
，椭圆
：
与双曲线
：
的焦点相同．
（1）求椭圆与双曲线的方程；
（2）过双曲线的右顶点作两条斜率分别为
，
的直线
，
，分别交双曲线于点
，
（，不同于右顶点），若
，求证：直线
的倾斜角为定值，并求出此定值；
（3）设点
，若对于直线
，椭圆上总存在不同的两点
与
关于直线
对称，且
，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】有以下说法:
①一年按365天计算,两名学生的生日相同的概率是
;②买彩票中奖的概率为0.001,那么买1 000张彩票就一定能中奖;③乒乓球赛前,决定谁先发球,抽签方法是从1~10共10个数字中各抽取1个,再比较大小,这种抽签方法是公平的;④昨天没有下雨,则说明“昨天气象局的天气预报降水概率是90%”是错误的.
根据我们所学的概率知识,其中说法正确的序号是___.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知集合A＝{x|2≤x≤8}，B＝{x|1<x<6}，C＝{x|x>a}，U＝R．
(1)求A∪B，(CUA)∩B；
(2)若A∩C≠
，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
.
(1)用分段函数的形式表示函数f(x)；
(2)在平面直角坐标系中画出函数f(x)的图象；
(3)在同一平面直角坐标系中，再画出函数g(x)＝
(x>0)的图象(不用列表)，观察图象直接写出当x>0时，不等式f(x)> 的解集．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
