【题目】在①函数
为奇函数；②当
时，
；③
是函数
的一个零点这三个条件中任选一个，补充在下面问题中，并解答，已知函数
，的图象相邻两条对称轴间的距离为
，______.
（1）求函数的解析式；
（2）求函数在
上的单调递增区间.
【答案】（1）选条件①②③任一个，均有
；（2）选条件①②③任一个，函数
在
上的单调递增区间均为
，
.
【解析】
（1）由相邻两条对称轴间的距离为
，得到
；再选择一个条件求解出
；
（2）由（1）解得的函数，根据复合函数的单调性得到单调区间.
解： 
函数的图象相邻对称轴间的距离为，
，
，
.
方案一：选条件①
为奇函数，
，
解得：
，
.
（1）
，
，
；
（2）由
，，
得
，，
令
，得
，令
，得
，
函数在上的单调递增区间为，；
方案二：选条件②
，
，
，或
，，
（1），，；
（2）由，，
得，，
令，得，令，得，
函数在上的单调递增区间为，；
方案三：选条件③
是函数的一个零点，
，
，.
（1），，；
（2）由，，得，
令，得，令，得.
函数在上的单调递增区间为，
黄冈创优卷系列答案科目：高中数学 来源： 题型：
【题目】如图所示，图①是棱长为1的小正方体，图②，③是由这样的小正方体摆放而成．按照这样的方法继续摆放，由上而下分别将第1层，第2层，…，第
层的小正方体的个数记为
，解答下列问题：
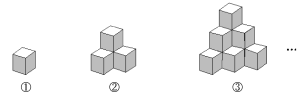
（1）按照要求填表：
| 1 | 2 | 3 | 4 | … |
| 1 | 3 | 6 | _ | … |
（2）
__________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【选修4-4：坐标系与参数方程】
在直角坐标系
中，曲线
的参数方程为
（
为参数），以坐标原点
为极点，
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
.
（Ⅰ）求曲线
的极坐标方程和
的直角坐标方程；
（Ⅱ）直线
与曲线
分别交于第一象限内的
，
两点，求
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若AC⊥BC，AC=BC=1，点P是△ABC内一点，则
的取值范围是（ ）
A. （﹣
，0） B. （0，） C. （﹣，） D. （﹣1，1）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若一个函数当自变量在不同范围内取值时，函数表达式不同，我们称这样的函数为分段函数．下面我们参照学习函数的过程与方法，探究分段函数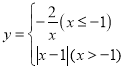
的图象与性质．列表：
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描点：在平面直角坐标系中，以自变量x的取值为横坐标，以相应的函数值y为纵坐标，描出相应的点，如图所示．
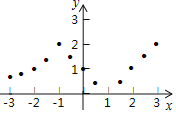
（1）如图，在平面直角坐标系中，观察描出的这些点的分布，作出函数图象；
（2）研究函数并结合图象与表格，回答下列问题：
①点
，
，
，
在函数图象上，
，
；（填“＞”，“＝”或“＜”）
②当函数值
时，求自变量x的值；
③在直线
的右侧的函数图象上有两个不同的点
，
，且
，求
的值；
④若直线
与函数图象有三个不同的交点，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】“杨辉三角”是我国数学史上的一个伟大成就，是二项式系数在三角形中的一种几何排列.如图所示，去除所有为1的项，依此构成数列2，3，3，4，6，4，5，10，10，5，…，则此数列的前56项和为_____.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】图是A，B两所学校艺术节期间收到的各类艺术作品的情况的统计图：
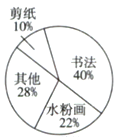
A学校 B学校
（1）从图中能否看出哪所学校收到的水粉画作品数量多？为什么？
（2）已知A学校收到的剪纸作品比B学校的多20件，收到的书法作品比B学校的少100件，请问这两所学校收到艺术作品的总数分别是多少件？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
