
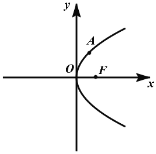
【题目】如图,在平面直角坐标系![]() 中,己知抛物线
中,己知抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 是第一象限内抛物线
是第一象限内抛物线![]() 上的一点,点
上的一点,点![]() 的坐标为
的坐标为![]()
(1)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)若![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)弦![]() 经过点
经过点![]() ,过弦
,过弦![]() 上一点
上一点![]() 作直线
作直线![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,求证:“直线
,求证:“直线![]() 与抛物线相切”的一个充要条件是“
与抛物线相切”的一个充要条件是“![]() 为弦
为弦![]() 的中点”.
的中点”.
【答案】(1)![]() (2)
(2)![]() (3)证明见解析
(3)证明见解析
【解析】
(1)因为点![]() 是第一象限内抛物线
是第一象限内抛物线![]() 上的一点,且
上的一点,且![]() ,设
,设![]() ,
,
则  即可求得答案;
即可求得答案;
(2)设![]() ,由
,由![]() ,
,![]() ,可得:
,可得:![]() ,
,![]() ,因为
,因为 ![]() ,可得
,可得![]() ,结合已知,即可求得答案;
,结合已知,即可求得答案;
(3)因为![]() 过点
过点![]() ,设
,设![]() 为:
为:![]() ,点
,点![]() ,点
,点![]() ,其
,其![]() 中点
中点![]() ,可得:
,可得:![]() ,联立直线与抛物线得
,联立直线与抛物线得![]() ,结合已知条件,根据充要条件定义,即可求得答案.
,结合已知条件,根据充要条件定义,即可求得答案.
(1)![]() 点
点![]() 是第一象限内抛物线
是第一象限内抛物线![]() 上的一点,且
上的一点,且![]()
设![]() ,
,
则 
解得: ,即
,即![]() .
.
(2)设![]() ,由
,由![]() ,
,![]()
可得:![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() ①
①
又![]()
![]() 等腰,得
等腰,得![]() 点在
点在![]() 轴投影为
轴投影为![]() 、
、![]() 中点,即:
中点,即:![]() .
.
将![]() ,
,![]() 代入①得:
代入①得:![]() ,
,![]() (舍去)
(舍去)
![]()
![]() 点坐标为
点坐标为![]() .
.
(3)![]()
![]() 过点
过点![]()
设![]() 为:
为:![]() ,点
,点![]() ,点
,点![]() ,其
,其![]() 中点
中点![]() ,
,
可得:![]()
联立直线与抛物线得![]() ,消掉
,消掉![]()
可得:![]()
根据韦达定理可得:![]()
![]()
![]()
设点![]() 处抛物线得切线为
处抛物线得切线为![]()
联立直线与抛物线得: ,消掉
,消掉![]()
可得:![]()
![]()
![]()
![]()
 ,可得:
,可得:![]()
![]() 过
过![]() 处切线方程为
处切线方程为![]()
化简得![]()
求切线![]() 与直线
与直线![]() 得交点
得交点![]()
可得![]()
![]()
![]() 轴,
轴,
![]() 与
与![]() 相切时,
相切时,![]() 为
为![]() 中点
中点
![]() 以上各步骤,均可逆
以上各步骤,均可逆
![]() “直线
“直线![]() 与抛物线相切”的一个充要条件是“
与抛物线相切”的一个充要条件是“![]() 为弦
为弦![]() 的中点”.
的中点”.


科目:高中数学 来源: 题型:
【题目】有着“中国碳谷”之称的安徽省淮北市,名优特产众多,其中“塔山石榴”因其青皮软籽、籽粒饱满、晶莹剔透、汁多味甘而享誉天下.现调查表明,石榴的甜度与海拔、日照时长、昼夜温差有着极强的相关性,分别用![]() 表示石榴甜度与海拔、日照时长、温差的相关程度,并对它们进行量化:0表示一般,1表示良,2表示优,再用综合指标
表示石榴甜度与海拔、日照时长、温差的相关程度,并对它们进行量化:0表示一般,1表示良,2表示优,再用综合指标![]() 的值评定石榴的等级,若
的值评定石榴的等级,若![]() 则为一级;若
则为一级;若![]() 则为二级;若
则为二级;若![]() 则为三级.
则为三级.![]() 近年来,周边各地市也开始发展石榴的种植,为了了解目前石榴在周边地市的种植情况,研究人员从不同地市随机抽取了12个石榴种植园,得到如下结果:
近年来,周边各地市也开始发展石榴的种植,为了了解目前石榴在周边地市的种植情况,研究人员从不同地市随机抽取了12个石榴种植园,得到如下结果:
种植园编号 | A | B | C | D | E | F |
|
|
|
|
|
|
|
种植园编号 | G | H | I | J | K | L |
|
|
|
|
|
|
|
(1)若有石榴种植园120个,估计等级为一级的石榴种植园的数量;
(2)在所取样本的二级和三级石榴种植园中任取2个,![]() 表示取到三级石榴种植园的数量,求随机变量
表示取到三级石榴种植园的数量,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 经过点
经过点![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围;
的取值范围;
(3)设直线![]() 和
和![]() 的斜率分别为
的斜率分别为![]() 和
和![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过多年的努力,炎陵黄桃在国内乃至国际上逐渐打开了销路,成为炎陵部分农民脱贫致富的好产品.为了更好地销售,现从某村的黄桃树上随机摘下了100个黄桃进行测重,其质量分布在区间![]() 内(单位:克),统计质量的数据作出其频率分布直方图如图所示:
内(单位:克),统计质量的数据作出其频率分布直方图如图所示:
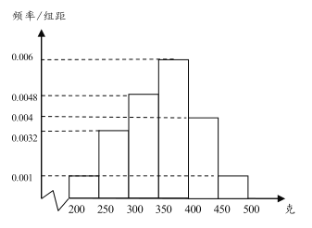
(1)按分层抽样的方法从质量落在![]() ,
,![]() 的黄桃中随机抽取5个,再从这5个黄桃中随机抽2个,求这2个黄桃质量至少有一个不小于400克的概率;
的黄桃中随机抽取5个,再从这5个黄桃中随机抽2个,求这2个黄桃质量至少有一个不小于400克的概率;
(2)以各组数据的中间数值代表这组数据的平均水平,以频率代表概率,已知该村的黄桃树上大约还有100000个黄桃待出售,某电商提出两种收购方案:
A.所有黄桃均以20元/千克收购;
B.低于350克的黄桃以5元/个收购,高于或等于350克的以9元/个收购.
请你通过计算为该村选择收益最好的方案.
(参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com