
 在平面几何中,三角形的面积可以通过公式:S三角形=
在平面几何中,三角形的面积可以通过公式:S三角形=| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
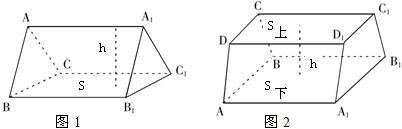 解:由三角形类比三棱柱,由平面图形面积类比立体图形的体积,结合求三角形面积的方法类比求三棱柱的体积:
解:由三角形类比三棱柱,由平面图形面积类比立体图形的体积,结合求三角形面积的方法类比求三棱柱的体积:| 1 |
| 2 |
| 1 |
| 2 |


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:高中数学 来源: 题型:
 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,AC=2
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,AC=2| 3 |
| 2S |
| l |
 C.
C.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2S |
| l |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| a上底+b下底 |
| 2 |
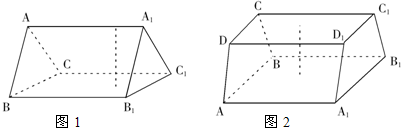
| 1 |
| 2 |
| 1 |
| 2 |
| S 上底+S 下底 |
| 2 |
| S 上底+S 下底 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ×a底×h高,S梯形=
×a底×h高,S梯形=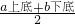 ×h高 来求得.
×h高 来求得.
查看答案和解析>>
科目:高中数学 来源:2007-2008学年江苏省南通市如东县高二(上)期末数学试卷(解析版) 题型:填空题
 a底h高来求得:类比到立体几何中,将一个侧面放置在水平面上的三棱柱(如图),其体积计算公式是 .
a底h高来求得:类比到立体几何中,将一个侧面放置在水平面上的三棱柱(如图),其体积计算公式是 .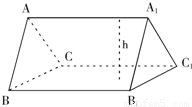
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com