
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行横道时,应当减速慢行;遇行人正在通过人行横道,应当停车让行,俗称“礼让斑马线”,《中华人民共和国道路交通安全法》 第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼让斑马线”行为统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
(1)请利用所给数据求违章人数![]() 与月份之间的回归直线方程
与月份之间的回归直线方程![]() ;
;
(2)交警从这5个月内通过该路口的驾驶员中随机抽查了50人,调查驾驶员不“礼让斑马线”行为与驾龄的关系,得到如下![]() 列联表:能否据此判断有
列联表:能否据此判断有![]() 的把握认为“礼让斑马线”行为与驾龄有关?
的把握认为“礼让斑马线”行为与驾龄有关?
不礼让斑马线 | 礼让斑马线 | 合计 | |
驾龄不超过1年 | 22 | 8 | 30 |
驾龄1年以上 | 8 | 12 | 20 |
合计 | 30 | 20 | 50 |
参考公式及数据:
 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() (其中
(其中![]() )
)
科目:高中数学 来源: 题型:
【题目】某果农选取一片山地种植红柚,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的![]() 倍.
倍.
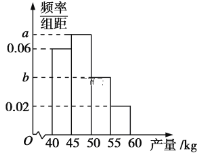
(1)求![]() 、
、![]() 的值;
的值;
(2)求样本的平均数;
(3)从样本中产量在区间(50,60]上的果树里随机抽取两株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
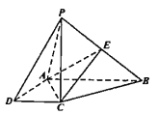
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() 是
是![]() 上的一点.
上的一点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,
的中点,![]() ,且直线
,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.己知圆
轴的正半轴为极轴建立极坐标系.己知圆![]() 的圆心的坐标为
的圆心的坐标为![]() 半径为
半径为![]() ,直线
,直线![]() 的参数方程为
的参数方程为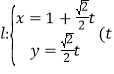 为参数)
为参数)
(Ⅰ)求圆C的极坐标方程;直线![]() 的普通方程;
的普通方程;
(Ⅱ)若圆C和直线![]() 相交于A,B两点,求线段AB的长.
相交于A,B两点,求线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 同时满足:(1)对于定义域内的任意
同时满足:(1)对于定义域内的任意![]() ,有
,有![]() ;(2)对于定义域内的任意
;(2)对于定义域内的任意![]() ,当
,当![]() 时,有
时,有![]() ,则称函数
,则称函数![]() 为“理想函数”.给出下列四个函数:①
为“理想函数”.给出下列四个函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④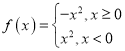 .
.
其中是“理想函数”的序号是( )
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值;
的距离的最大值;
(2)若曲线![]() 上的所有点都在直线
上的所有点都在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数.
为奇函数.
(1)求a的值,并证明![]() 是R上的增函数;
是R上的增函数;
(2)若关于t的不等式f(t2-2t)+f(2t2-k)<0的解集非空,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随机抽取![]() 人对共享产品对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的
人对共享产品对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的![]() 人中的性别以及意见进行了分类,得到的数据如下表所示:
人中的性别以及意见进行了分类,得到的数据如下表所示:
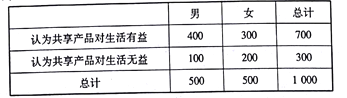
(Ⅰ)根据表中的数据,能否在犯错的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(Ⅱ)现按照分层抽样从认为共享产品增多对生活无益的人员中随机抽取![]() 人,再从
人,再从![]() 人中随机抽取
人中随机抽取![]() 人赠送超市购物券作为答谢,求恰有
人赠送超市购物券作为答谢,求恰有![]() 人是女性的概率.
人是女性的概率.
参考公式: 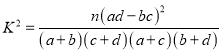 .
.
临界值表:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com