
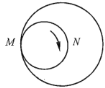
【题目】如图,一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方向滚动,M和N是小圆的一条固定直径的两个端点,那么,当小圆这样滚过大圆内壁的一周,点M,N在大圆内所绘出的图形大致是( )
A.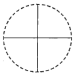 B.
B.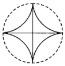 C.
C.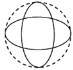 D.
D.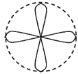
【答案】A
【解析】
设某时刻两圆相切于点![]() ,此时动点
,此时动点![]() 所处的位置为点
所处的位置为点![]() ,以切点
,以切点![]() 在如图上运动为例,记直线
在如图上运动为例,记直线![]() 与此时小圆
与此时小圆![]() 的交点为
的交点为![]() ,利用弧长公式计算,可知小圆的圆弧
,利用弧长公式计算,可知小圆的圆弧![]() 与圆弧
与圆弧![]() 的长相等,可得点
的长相等,可得点![]() 与点
与点![]() 重合,即动点
重合,即动点![]() 在线段
在线段![]() 上运动,同理可知,此时点
上运动,同理可知,此时点![]() 在与
在与![]() 垂直的线段上运动,再通过观察四个选项可得答案.
垂直的线段上运动,再通过观察四个选项可得答案.
如图所示:
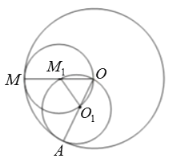
由题意可知,小圆![]() 总与大圆
总与大圆![]() 相内切,且小圆
相内切,且小圆![]() 总经过大圆的圆心
总经过大圆的圆心![]() ,
,
设某时刻两圆相切于点![]() ,此时动点
,此时动点![]() 所处的位置为点
所处的位置为点![]() ,
,
则大圆圆弧![]() 与小圆
与小圆![]() 转过的圆弧相等,
转过的圆弧相等,
以切点![]() 在如图上运动为例,记直线
在如图上运动为例,记直线![]() 与此时小圆
与此时小圆![]() 的交点为
的交点为![]() ,
,
记![]() ,则
,则![]() ,
,
所以![]()
![]() ,
,
所以大圆圆弧![]() 的长为
的长为![]() ,小圆圆弧
,小圆圆弧![]() 的长为
的长为![]() ,
,
所以![]() ,
,
所以小圆的圆弧![]() 与圆弧
与圆弧![]() 的长相等,
的长相等,
所以点![]() 与点
与点![]() 重合,即动点
重合,即动点![]() 在线段
在线段![]() 上运动,
上运动,
同理可知,此时点![]() 在与
在与![]() 垂直的线段上运动,
垂直的线段上运动,
点![]() 在其它位置类似可得,
在其它位置类似可得,![]() 、
、![]() 的轨迹为互相垂直的线段.
的轨迹为互相垂直的线段.
观察四个选项可知,只有选项![]() 符合.
符合.
故选:A.


科目:高中数学 来源: 题型:
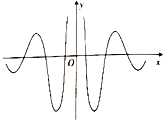
【题目】著名数学家华罗庚先生曾说过:“数缺形时少直观,形缺数时难入微数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,我们经常用函数的图象来研究函数的性质,也经常用函数的解析式来琢磨函数的图象的特征,如某体育品牌的LOGO为![]() ,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|﹣|2x﹣2|的最大值为M,正实数a,b满足a+b=M.
(1)求2a2+b2的最小值;
(2)求证:aabb≥ab.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)若函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() ,求实数a的值;
,求实数a的值;
(2)若函数![]() 有2个不同的零点
有2个不同的零点![]() ,
,![]() .
.
①求实数a的取值范围;
②求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机调查某城市80名有子女在读小学的成年人,以研究晚上八点至十点时间段辅导子女作业与性别的关系,得到下面的数据表:
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 60 | |
女 | |||
合计 | 40 | 80 |
(1)请将表中数据补充完整;
(2)用样本的频率估计总体的概率,估计这个城市有子女在读小学的成人女性晚上八点至十点辅导子女作业的概率;
(3)根据以上数据,能否有99%以上的把握认为“晚上八点至十点时间段是否辅导子女作业与性别有关?”.
参考公式: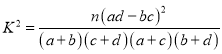 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)求 函数![]() 的单调区间;
的单调区间;
(2)定义:对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的不动点. 如果函数
的不动点. 如果函数![]() 存在两个不同的不动点,求实数
存在两个不同的不动点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某公司五类机器的销售情况,该公司随机收集了一个月销售的有关数据,公司规定同一类机器销售价格相同,经分类整理得到下表:
机器类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 |
销售总额(万元) |
|
|
|
|
|
销售量(台) |
|
|
|
|
|
利润率 |
|
|
|
|
|
利润率是指:一台机器销售价格减去出厂价格得到的利润与该机器销售价格的比值.
(Ⅰ)从该公司本月卖出的机器中随机选一台,求这台机器利润率高于0.2的概率;
(Ⅱ)从该公司本月卖出的销售单价为20万元的机器中随机选取![]() 台,求这两台机器的利润率不同的概率;
台,求这两台机器的利润率不同的概率;
(Ⅲ)假设每类机器利润率不变,销售一台第一类机器获利![]() 万元,销售一台第二类机器获利
万元,销售一台第二类机器获利![]() 万元,…,销售一台第五类机器获利
万元,…,销售一台第五类机器获利![]() ,依据上表统计数据,随机销售一台机器获利的期望为
,依据上表统计数据,随机销售一台机器获利的期望为![]() ,设
,设![]() ,试判断
,试判断![]() 与
与![]() 的大小.(结论不要求证明)
的大小.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
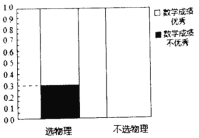
【题目】某省即将实行新高考,不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响,对该校2018级的1000名学生进行调查,收集到相关数据如下:
(1)根据以上提供的信息,完成![]() 列联表,并完善等高条形图;
列联表,并完善等高条形图;
选物理 | 不选物理 | 总计 | |
数学成绩优秀 | |||
数学成绩不优秀 | 260 | ||
总计 | 600 | 1000 |
(2)能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关?
附: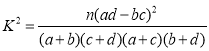
临界值表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com