
分析 不等式x2+2ax+1≥0对于一切x∈(0,$\frac{1}{2}$]恒成立,转化为a≥-$\frac{1}{2}$x-$\frac{1}{2x}$对于一切x∈(0,$\frac{1}{2}$]恒成立,求出-$\frac{1}{2}$x-$\frac{1}{2x}$的最大值即可.
解答 解:当x∈(0,$\frac{1}{2}}$]时,
不等式x2+2ax+1≥0可化为a≥-$\frac{1}{2}$x-$\frac{1}{2x}$,
设f(x)=-$\frac{1}{2}$x-$\frac{1}{2x}$,x∈(0,$\frac{1}{2}}$],
且函数f(x)在x∈(0,$\frac{1}{2}}$]上是单调增函数,
最大值是f($\frac{1}{2}$)=-$\frac{1}{2}$×$\frac{1}{2}$-$\frac{1}{2×\frac{1}{2}}$=-$\frac{5}{4}$,
∴a的最小值是-$\frac{5}{4}$.
故答案为:$-\frac{5}{4}$.
点评 本题考查了不等式的恒成立问题,也考查了函数的单调性运用问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
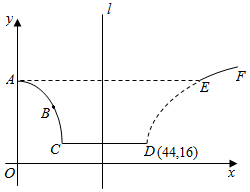 在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线的变化情况来决定买入或卖出股票.股民老张在研究股票的走势图时,发现一只股票的均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xOy,则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+φ)+b(0<φ<π)来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线l:x=34对称.老张预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线l对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F.现在老张决定取点A(0,22),点B(12,19),点D(44,16)来确定解析式中的常数a,b,ω,φ,并且求得ω=$\frac{π}{72}$
在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线的变化情况来决定买入或卖出股票.股民老张在研究股票的走势图时,发现一只股票的均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xOy,则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+φ)+b(0<φ<π)来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线l:x=34对称.老张预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线l对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F.现在老张决定取点A(0,22),点B(12,19),点D(44,16)来确定解析式中的常数a,b,ω,φ,并且求得ω=$\frac{π}{72}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,4] | B. | [2,3] | C. | [-2,4] | D. | [-2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com