【答案】
分析:首先设出向量
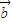
的坐标(x,y),然后根据|
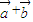
|=3列关于x、y的表达式,运用该式几何意义得知以原点为起点的向量
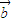
的终点的位置,数形结合可求解
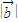
的取值范围.
解答:解:设
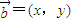
,则
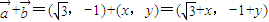
,
由|
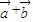
|=3得,
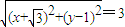
,即
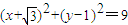
,
所以以原点为起点的向量
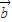
的终点在以(-
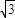
,1)为圆心,以3为半径的圆周上,又原点到圆心的距离为
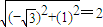
,
所以
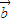
的模的最小值为圆的半径减去原点到圆心的距离,为3-2=1,
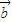
的模的最大值为圆的半径加上原点到圆心的距离,为3+2=5,
则
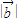
的取值范围是[1,5].
故选D.
点评:本题考查向量模的范围的求解方法,考查了数形结合的解题思想,特别是在得到方程即
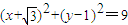
后,能明确以原点为起点的向量
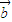
的终点的位置.

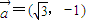 ,且向量
,且向量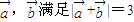 ,则
,则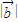 的取值范围是( )
的取值范围是( )