
【题目】已知向量 ![]() =(sin
=(sin ![]() ,sin
,sin ![]() ),
), ![]() =(cos
=(cos ![]() ,cos
,cos ![]() ),且向量
),且向量 ![]() 与向量
与向量 ![]() 共线.
共线.
(1)求证:sin( ![]() ﹣
﹣ ![]() )=0;
)=0;
(2)若记函数f(x)=sin( ![]() ﹣
﹣ ![]() ),求函数f(x)的对称轴方程;
),求函数f(x)的对称轴方程;
(3)求f(1)+f(2)+f(3)+…+f(2013)的值;
(4)如果已知角0<A<B<π,且A+B+C=π,满足f( ![]() )=f(
)=f( ![]() )=
)= ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)证明:∵向量 ![]() 与向量
与向量 ![]() 共线,
共线,
∴sin ![]() cos
cos ![]() ﹣sin
﹣sin ![]() cos
cos ![]() =0,即sin(
=0,即sin( ![]() ﹣
﹣ ![]() )=0
)=0
(2)解:由 ![]() (k∈Z)得,
(k∈Z)得, ![]() ,
,
∴函数f(x)的对称轴方程是 ![]()
(3)由f(x)=sin( ![]() ﹣
﹣ ![]() )得,函数f(x)的周期T=
)得,函数f(x)的周期T= ![]() =4,
=4,
则f(1)+f(2)+f(3)+f(4)= ![]() =0,
=0,
∴f(1)+f(2)+f(3)+…+f(2013)=503×[f(1)+f(2)+f(3)+f(4)]+ ![]() =
= ![]()
(4)由f( ![]() )=f(
)=f( ![]() )=
)= ![]() 得,
得, ![]() ,
,
∵0<A<B<π,∴ ![]() ,
, ![]() ,
,
则 ![]() ,
, ![]() ,
,
解得,A= ![]() ,B=
,B= ![]() ,
,
由A+B+C=π得,C= ![]() ,
,
∴ 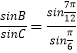 =2sin(
=2sin( ![]() )=
)= ![]()
【解析】(1)根据向量共线的条件和两角差的正弦公式化简即可;(2)根据正弦函数的对称轴得: ![]() (k∈Z),再求出x的式子得函数f(x)的对称轴方程;(3)先由周期公式求出函数的周期,再求出一个周期内的函数值的和,然后判断出式子中共有多少个周期,再求出式子的值;(4)把条件代入解析式化简后,根据角的范围求出A、B的值,再求出C的值,代入式子根据两角和的正弦公式化简求值.
(k∈Z),再求出x的式子得函数f(x)的对称轴方程;(3)先由周期公式求出函数的周期,再求出一个周期内的函数值的和,然后判断出式子中共有多少个周期,再求出式子的值;(4)把条件代入解析式化简后,根据角的范围求出A、B的值,再求出C的值,代入式子根据两角和的正弦公式化简求值.
【考点精析】解答此题的关键在于理解两角和与差的正弦公式的相关知识,掌握两角和与差的正弦公式:![]() ,以及对正弦函数的对称性的理解,了解正弦函数的对称性:对称中心
,以及对正弦函数的对称性的理解,了解正弦函数的对称性:对称中心![]() ;对称轴
;对称轴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,已知点![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为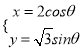 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,点
轴正半轴为极轴,建立极坐标系,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且
,且![]() 过点
过点![]() ;过点
;过点![]() 与直线
与直线![]() 平行的直线为
平行的直线为![]() ,
, ![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() .
.
(1)求曲线![]() 上的点到直线
上的点到直线![]() 距离的最小值;
距离的最小值;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
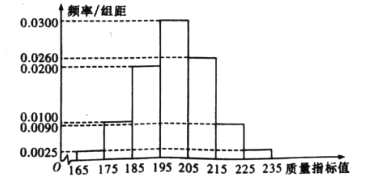
(1)根据以上抽样调查数据 ,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(2)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() :
: ![]() ,曲线
,曲线![]() :
: ![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(Ⅰ)求曲线![]() ,
, ![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)曲线![]() :
: ![]() (
(![]() 为参数,
为参数, ![]() ,
, ![]() )分别交
)分别交![]() ,
, ![]() 于
于![]() ,
, ![]() 两点,当
两点,当![]() 取何值时,
取何值时, ![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面向量 ![]() =(1,x),
=(1,x), ![]() =(2x+3,﹣x)(x∈R).
=(2x+3,﹣x)(x∈R).
(1)若 ![]() ∥
∥ ![]() ,求|
,求| ![]() |
|
(2)若 ![]() 与
与 ![]() 夹角为锐角,求x的取值范围.
夹角为锐角,求x的取值范围.
(3)若| ![]() |=2,求与
|=2,求与 ![]() 垂直的单位向量
垂直的单位向量 ![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B,C,D为平面内的四点,且A(1,3),B(2,﹣2),C(4,1).
(1)若 ![]() =
= ![]() ,求D点的坐标;
,求D点的坐标;
(2)设向量 ![]() =
= ![]() ,
, ![]() =
= ![]() ,若k
,若k ![]() ﹣
﹣ ![]() 与
与 ![]() +3
+3 ![]() 平行,求实数k的值.
平行,求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足an=2Sn﹣1(n∈N*) (Ⅰ)求证:数列{an}为等比数列;
(Ⅱ)若bn=(2n+1)an , 求{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】节能减排以来,兰州市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图. 
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)估计用电量落在[220,300)中的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com