
【题目】有以下命题:
①对任意的α∈R都有sin3α=3sinα﹣4sin3α成立;
②对任意的△ABC都有等式a=bcosA+ccosB成立;
③满足“三边是连续的三个正整数且最大角是最小的2倍”的三角形存在且唯一;
④若A,B是钝角△ABC的二锐角,则sinA+sinB<cosA+cosB.
其中正确的命题的个数是( )
A.4
B.3
C.2
D.1
【答案】A
【解析】解:①对任意的α∈R都有sin3α=sin(α+2α)
=sinαcos2α+cosαsin2α
=sinα(cos2α﹣sin2α)+2sinαcos2α
=sinα(1﹣2sin2α)+2sinα(1﹣sin2α)
=3sinα﹣4sin3α,
故①正确;
②对任意的△ABC都有 ![]() =2R,
=2R,
∴a=2RsinA
=2Rsin(B+C)
=2RsinBcosC+2RsinCcosB
=bcosC+ccosB,
故②正确;
③假设存在正整数k、k+1、k﹣1分别为三角形ABC的三边长,
且其对应的角分别为A、B、C,
∴ ![]() =2R,
=2R,
∵B=2C,
∴sinB=sin2C=2sinCcosC,
∴ ![]() =
= ![]() ,即cosC=
,即cosC= ![]() +
+ ![]() ,
,
又∵C<A<B,即C<A<2C,
∴36°<C<45°,
∴ ![]() <cosC<
<cosC< ![]() ,即
,即 ![]() <
< ![]() +
+ ![]() <
< ![]() ,
,
∴ ![]() ﹣
﹣ ![]() <
< ![]() <
< ![]() ﹣
﹣ ![]() ,
,
∴ ![]() +1<k﹣1<
+1<k﹣1< ![]() 2,
2,
∴ ![]() +2<k<
+2<k< ![]() 3,
3,
∴k=4或k=5,
经检验可知当k=5时不满足题意,
故③正确;
④∵A,B是钝角△ABC的二锐角,
∴A+B<90°,
∴0°<B<90°﹣A<90°,
∴sinB<sin(90°﹣A)=cosB,
同理cosA>cos(90°﹣B)=sinA,
∴sinA+sinB<cosA+cosB,
故④正确;
故选:A.
【考点精析】通过灵活运用命题的真假判断与应用,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系即可以解答此题.


科目:高中数学 来源: 题型:
【题目】![]() . 问:是否存在正数m,使得对于任意正数
. 问:是否存在正数m,使得对于任意正数![]() ,可使
,可使![]() 为三角形的三边构成三角形?如果存在:①试写出一组x,y,m的值,②求出所有m的值;如果不存在,请说明理由.
为三角形的三边构成三角形?如果存在:①试写出一组x,y,m的值,②求出所有m的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出x(x∈N*)名员工从事第三产业,调整后他们平均每人每年创造利润为10(a﹣ ![]() )万元(a>0),剩下的员工平均每人每年创造的利润为原来(1+
)万元(a>0),剩下的员工平均每人每年创造的利润为原来(1+ ![]() )倍.
)倍.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多可以整出多少名员工从事第三产业;
(2)若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,则a的最大取值是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为选拔参加“央视猜灯谜大赛”的队员,在校内组织猜灯谜竞赛.规定:第一阶段知识测试成绩不小于![]() 分的学生进入第二阶段比赛.现有
分的学生进入第二阶段比赛.现有![]() 名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
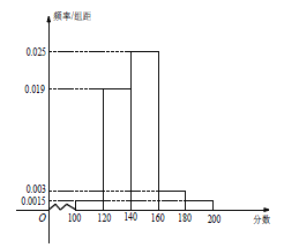
(1)估算这![]() 名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
(2)将进入第二阶段的学生分成若干队进行比赛.现甲、乙两队在比赛中均已获得![]() 分,进入最后强答阶段.抢答规则:抢到的队每次需猜
分,进入最后强答阶段.抢答规则:抢到的队每次需猜![]() 条谜语,猜对
条谜语,猜对![]() 条得
条得![]() 分,猜错
分,猜错![]() 条扣
条扣![]() 分.根据经验,甲队猜对每条谜语的概率均为
分.根据经验,甲队猜对每条谜语的概率均为![]() ,乙队猜对每条谜语的概率均为
,乙队猜对每条谜语的概率均为![]() ,猜对第
,猜对第![]() 条的概率均为
条的概率均为![]() .若这两条抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
.若这两条抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,tanA是以﹣4为第三项,4为第七项的等差数列的公差,tanB是以2为公差,9为第五项的等差数列的第二项,则这个三角形是( )
A.锐角三角形
B.钝角三角形
C.等腰直角三角形
D.等腰或直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系![]() 中曲线
中曲线![]() 经伸缩变换
经伸缩变换![]() 后得到曲线
后得到曲线![]() ,在以
,在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的参数方程和
的参数方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的一点,又
上的一点,又![]() 向曲线
向曲线![]() 引切线,切点为
引切线,切点为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取![]() 名学生的成绩进行统计,作出的茎叶图如下图,记成绩不低于
名学生的成绩进行统计,作出的茎叶图如下图,记成绩不低于![]() 分者为“成绩优良”.
分者为“成绩优良”.

(1)分别计算甲、乙两班![]() 个样本中,化学分数前十的平均分,并据此判断哪种教学方式的教学效果更
个样本中,化学分数前十的平均分,并据此判断哪种教学方式的教学效果更
佳;
(2)甲、乙两班![]() 个样本中,成绩在
个样本中,成绩在![]() 分以下(不含
分以下(不含![]() 分)的学生中任意选取
分)的学生中任意选取![]() 人,求这
人,求这![]() 人来自不同班级的概率;
人来自不同班级的概率;
(3)由以上统计数据填写下面![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为“成绩优良与教学方式有关”?
的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
附: 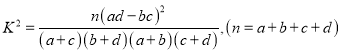
独立性检验临界值表:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com