
| A. | a>b>c | B. | c>b>a | C. | c<a<b | D. | a>c>b |
分析 设g(x)=xf(x),由导数性质推导出当x∈(-∞,0)单调递减,再根据函数的奇偶性得到x∈(0,+∞)时,函数y=g(x)单调递减.由此能求出结果
解答 解:∵设g(x)=xf(x)
∴g′(x)=[xf(x)]'=f(x)+xf'(x),
∴当x∈(-∞,0)时,g′(x)=f(x)+xf'(x)<0,函数y=g(x)单调递减,
∵f(x)满足f(x)=f(-x),
∴函数y=f(x)为偶函数,
∴函数y=g(x)为奇函数,
∴当x∈(0,+∞)时,函数y=g(x)单调递减.
∴20.1>1,0<ln2<1,log2$\frac{1}{8}$=-3,
∴g(-3)=g(3),
∴g(-3)<g(20.1)<g(ln2),
∴c<a<b,
故选:C.
点评 本题考查三个数的大小的比较,解题时要认真审题,注意导数性质、函数性质的合理运用,属于中档题


科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | ($\frac{1}{e}$,1) | C. | (2,3) | D. | (e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | lg(x2+1)≥0 | B. | 5≤2 | C. | 若x2=4,则x=2 | D. | 若x<2,则$\frac{1}{x}$>$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 科研费用x(百万元) | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 |
| 公司所获利润y(百万元) | 1 | 1.5 | 2 | 2.5 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
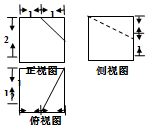
| A. | 4cm2 | B. | $\frac{43}{2}$cm2 | C. | 23cm2 | D. | 24cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com