
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)求证:直线![]() 是曲线
是曲线![]() 的切线;
的切线;
(Ⅲ)写出![]() 的一个值,使得函数
的一个值,使得函数![]() 有三个不同零点(只需直接写出数值)
有三个不同零点(只需直接写出数值)
【答案】(1)递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() ; (2)见解析;(3)见解析.
; (2)见解析;(3)见解析.
【解析】
(Ⅰ)当a=﹣1时,求f(x)的导数f′(x),由f′(x)>0,得f(x)单调递增;f′(x)<f(x)单调递减;
(Ⅱ)由f′(x)=3x2+2x+a,令f′(x)=)=3x2+2x+a=a,解得x1=0,x2=![]() ,
,
而f(0)=﹣1,曲线y=f(x)在点(0,f(0))处的切线方程为y=ax﹣1,由此可得,无论a为何值,直线y=ax﹣1是曲线y=f(x)在点(0,f(0))处的切线;(Ⅲ)取a的值为﹣2.
(Ⅰ)函数![]() 的定义域为
的定义域为![]()
当a=-1时,![]()
所以![]()
令![]() ,得
,得![]() ,
,![]()
当x变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
x |
| -1 |
|
|
|
| + | 0 | - | 0 | + |
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]()
(Ⅱ)因为![]()
令![]() ,解得
,解得![]() ,
,![]()
而![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即所以无论a为何值,直线![]() 都是曲线
都是曲线![]() 在点
在点![]() 处的切线
处的切线
(Ⅲ)取a的值为-2这里a的值不唯一,只要取a的值小于-1即可.


科目:高中数学 来源: 题型:
【题目】某快递公司(为企业服务)准备在两种员工付酬方式中选择一种现邀请甲、乙两人试行10天两种方案如下:甲无保底工资送出50件以内(含50件)每件支付3元,超出50件的部分每件支付5元;乙每天保底工资50元,且每送出一件再支付2元分别记录其10天的件数得到如图茎叶图,若将频率视作概率,回答以下问题:

(1)记甲的日工资额为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)如果仅从日工资额的角度考虑请利用所学的统计学知识为快递公司在两种付酬方式中作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的圆心在直线![]() :
:![]() 上,与直线
上,与直线![]() :
:![]() 相切,截直线
相切,截直线![]() :
:![]() 所得的弦长为6.
所得的弦长为6.
(1)求圆M的方程;
(2)过点![]() 的两条成
的两条成![]() 角的直线分别交圆M于A,C和B,D,求四边形
角的直线分别交圆M于A,C和B,D,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (其中e为自然对数的底数,m、n为常数),函数
(其中e为自然对数的底数,m、n为常数),函数![]() 定义为:对每一个给定的实数x,
定义为:对每一个给定的实数x,
(1)当m、n满足什么条件时,![]() 对所有的实数x恒成立;
对所有的实数x恒成立;
(2)设a、b是两个实数,满足![]() 且m,
且m,![]() 当
当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 的上的单调增区间的长度之和(用含a、b的式子表示)(闭区间
的上的单调增区间的长度之和(用含a、b的式子表示)(闭区间![]() 的长度定义为
的长度定义为![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰好有一个元素,求实数
的解集中恰好有一个元素,求实数![]() 的值;
的值;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过
上的最大值与最小值的差不超过![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某新建小区规划利用一块空地进行配套绿化.已知空地的一边是直路![]() ,余下的外围是抛物线的一段弧,直路
,余下的外围是抛物线的一段弧,直路![]() 的中垂线恰是该抛物线的对称轴(如图),点O是
的中垂线恰是该抛物线的对称轴(如图),点O是![]() 的中点.拟在这个地上划出一个等腰梯形
的中点.拟在这个地上划出一个等腰梯形![]() 区域种植草坪,其中
区域种植草坪,其中![]() 均在该抛物线上.经测量,直路
均在该抛物线上.经测量,直路![]() 长为60米,抛物线的顶点P到直路
长为60米,抛物线的顶点P到直路![]() 的距离为60米.设点C到抛物线的对称轴的距离为m米,到直路
的距离为60米.设点C到抛物线的对称轴的距离为m米,到直路![]() 的距离为n米.
的距离为n米.

(1)求出n关于m的函数关系式.
(2)当m为多大时,等腰梯形草坪![]() 的面积最大?并求出其最大值.
的面积最大?并求出其最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD为直角梯形,AD//BC,且![]() ,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为等边三角形,M是棱PC上的一点,设
,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为等边三角形,M是棱PC上的一点,设![]() (M与C不重合).
(M与C不重合).
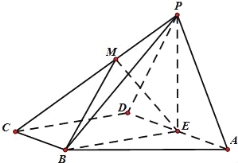
(1)求证:CD⊥DP;
(2)若PA∥平面BME,求k的值;
(3)若二面角M﹣BE﹣A的平面角为150°,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有10名员工,他们某年的收入如下表:
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪(万元) | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
(1)求该单位员工当年年薪的平均值和中位数;
(2)已知员工年薪收入与工作年限成正相关关系,某员工工作第一年至第四年的年薪分别为4万元、5.5万元、6万元、8.5万元,预测该员工第六年的年薪为多少?
附:线性回归方程![]() 中系数计算公式分别为:
中系数计算公式分别为: ,
,![]() ,其中
,其中![]() 、
、![]() 为样本均值.
为样本均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com