
【题目】已知椭圆![]() 和直线
和直线![]() :
: ![]() ,椭圆的离心率
,椭圆的离心率![]() ,坐标原点到直线
,坐标原点到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)已知定点![]() ,若直线
,若直线![]() 过点
过点![]() 且与椭圆相交于
且与椭圆相交于![]() 两点,试判断是否存在直线
两点,试判断是否存在直线![]() ,使以
,使以![]() 为直径的圆过点
为直径的圆过点![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.

【答案】(I)![]() ;(II)
;(II)![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)根据椭圆中的![]() ,以及
,以及![]() ,和点到直线的距离公式计算求得
,和点到直线的距离公式计算求得![]() ;(Ⅱ)分斜率不存在和斜率存在两种情况讨论,当斜率存在时,设直线为
;(Ⅱ)分斜率不存在和斜率存在两种情况讨论,当斜率存在时,设直线为![]() 与椭圆方程联立,利用根与系数的关系计算
与椭圆方程联立,利用根与系数的关系计算![]() ,从而求得斜率
,从而求得斜率![]() 和直线方程.
和直线方程.
试题解析:(Ⅰ)由直线![]() ,∴
,∴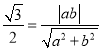 ,即
,即![]() ——①
——①
又由![]() ,得
,得![]() ,即
,即![]() ,又∵
,又∵![]() ,∴
,∴![]() ——②
——②
将②代入①得,即![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() ,
,
∴所求椭圆方程是![]() ;
;
(Ⅱ)①当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 方程为
方程为![]() ,
,
则直线![]() 与椭圆的交点为
与椭圆的交点为![]() ,又∵
,又∵![]() ,
,
∴![]() ,即以
,即以![]() 为直径的圆过点
为直径的圆过点![]() ;
;
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 方程为
方程为![]() ,
, ![]() ,
, ![]() ,
,
由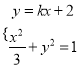 ,得
,得![]() ,
,
由![]() ,得
,得![]() 或
或![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]()
∵以![]() 为直径的圆过点
为直径的圆过点![]() ,∴
,∴![]() ,即
,即![]() ,
,
由![]() ,
, ![]() ,
,
得![]() ,∴
,∴![]() ,
,
∴![]() ,解得
,解得![]() ,即
,即![]() ;
;
综上所述,当以![]() 为直径的圆过定点
为直径的圆过定点![]() 时,直线
时,直线![]() 的方程为
的方程为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)=﹣x2+ax﹣2.
(1)若曲线f(x)=xlnx在x=1处的切线与函数g(x)=﹣x2+ax﹣2也相切,求实数a的值;
(2)求函数f(x)在![]() 上的最小值;
上的最小值;
(3)证明:对任意的x∈(0,+∞),都有![]() 成立
成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
⑴求椭圆![]() 的标准方程;
的标准方程;
⑵已知动直线![]() 过点
过点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() 两点.试问
两点.试问![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下五个命题:
①在线性回归模型中, ![]() 表示解释变量对于预报变量变化的贡献率,在对女大学生的身高预报体重的回归分析数据中,算得
表示解释变量对于预报变量变化的贡献率,在对女大学生的身高预报体重的回归分析数据中,算得![]() ,表明“女大学生的体重差异有64%是由身高引起的”
,表明“女大学生的体重差异有64%是由身高引起的”
②随机变量的方差和标准差都反映了随机变量取值偏离于均值的平均程度,方差或标准差越小,则随机变量偏离于均值的平均程度越大;
③正态曲线关于直线![]() 对称,这个曲线只有当
对称,这个曲线只有当![]() 时,才在
时,才在![]() 轴上方;
轴上方;
④正态曲线的对称轴由![]() 确定,当
确定,当![]() 一定时,曲线的形状由
一定时,曲线的形状由![]() 决定,并且
决定,并且![]() 越大,曲线越“矮胖”;
越大,曲线越“矮胖”;
⑤若随机变量![]() ,且
,且![]() 则
则![]() ;
;
其中正确命题的序号是
A. ②③ B. ①④⑤ C. ①④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(数学文卷·2017届湖北省黄冈市高三上学期期末考试第16题) “中国剩余定理”又称“孙子定理”.1852年英国来华传教伟烈亚利将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”. “中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将2至2017这2016个数中能被3除余1且被5除余1的数按由小到大的顺序排成一列,构成数列![]() ,则此数列的项数为__________.
,则此数列的项数为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个三角形的平行投影仍是三角形,则下列命题:
①三角形的高线的平行投影,一定是这个三角形的平行投影的高线;
②三角形的中线的平行投影,一定是这个三角形的平行投影的中线;
③三角形的角平分线的平行投影,一定是这个三角形的平行投影的角平分线;
④三角形的中位线的平行投影,一定是这个三角形的平行投影的中位线.
其中正确的命题有 ( )
A. ①② B. ②③
C. ③④ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com