
【题目】已知命题p:k2﹣8k﹣20≤0,命题q:方程![]() 1表示焦点在x轴上的双曲线.
1表示焦点在x轴上的双曲线.
(1)命题q为真命题,求实数k的取值范围;
(2)若命题“p∨q”为真,命题“p∧q”为假,求实数k的取值范围.
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为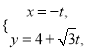 (
(![]() 为参数),曲线
为参数),曲线![]() 的方程为
的方程为![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线![]() 和曲线
和曲线![]() 的极坐标方程;
的极坐标方程;
(2)曲线![]() 分别交直线
分别交直线![]() 和曲线
和曲线![]() 于点
于点![]() ,求
,求![]() 的最大值及相应
的最大值及相应![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体ABCD-A1B1C1D1的棱长为2,E为棱CC1的中点,点M在正方形BCC1B1内运动,且直线AM//平面A1DE,则动点M 的轨迹长度为( )
A. ![]() B. π C. 2 D.
B. π C. 2 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .斜率为k的直线l与椭圆M有两个不同的交点A,B.
.斜率为k的直线l与椭圆M有两个不同的交点A,B.
(Ⅰ)求椭圆M的方程;
(Ⅱ)若![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)设![]() ,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点
,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点![]() 共线,求k.
共线,求k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四组函数中,表示同一函数的是
A.f(x)=![]()
![]() ,g(x)=x2–1B.f(x)=
,g(x)=x2–1B.f(x)=![]() ,g(x)=x+1
,g(x)=x+1
C.f(x)=![]() ,g(x)=(
,g(x)=(![]() )2D.f(x)=|x|,g(t)=
)2D.f(x)=|x|,g(t)=![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为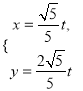 (
(![]() 为参数),以平面直角坐标系的原点为极点,正半轴为极轴,取相同的长度单位建立极坐标系,曲线
为参数),以平面直角坐标系的原点为极点,正半轴为极轴,取相同的长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程,并指明曲线
的直角坐标方程,并指明曲线![]() 的形状;
的形状;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,
两点, ![]() 为坐标原点,且
为坐标原点,且![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业常年生产一种出口产品,根据预测可知,进入21世纪以来,该产品的产量平稳增长.记2009年为第1年,且前4年中,第x年与年产量f(x) 万件之间的关系如下表所示:
x | 1 | 2 | 3 | 4 |
f(x) | 4.00 | 5.58 | 7.00 | 8.44 |
若f(x)近似符合以下三种函数模型之一:f(x)=ax+b,f(x)=2x+a,f(x)=log![]() x+a.
x+a.
(1)找出你认为最适合的函数模型,并说明理由,然后选取其中你认为最适合的数据求出相应的解析式;
(2)因遭受某国对该产品进行反倾销的影响,2015年的年产量比预计减少30%,试根据所建立的函数模型,确定2015年的年产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C: ![]() ,定义椭圆C的“相关圆”方程为
,定义椭圆C的“相关圆”方程为![]() ,若抛物线
,若抛物线![]() 的焦点与椭圆C的一个焦点重合,且椭圆C短轴的一个端点和其两个焦点构成直角三角形。
的焦点与椭圆C的一个焦点重合,且椭圆C短轴的一个端点和其两个焦点构成直角三角形。
(I)求椭圆C的方程和“相关圆”E的方程;
(II)过“相关圆”E上任意一点P作“相关圆”E的切线l与椭圆C交于A,B两点,O为坐标原点。
(i)证明∠AOB为定值;
(ii)连接PO并延长交“相关圆”E于点Q,求△ABQ面积的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com