
【题目】已知集合A={x|﹣2≤x≤5},B={x|m﹣4≤x≤3m+3}.
(1)若AB,求实数m的取值范围;
(2)若A∩B=B,求实数m的取值范围.
【答案】
(1)解:∵集合A={x|﹣2≤x≤5},B={x|m﹣4≤x≤3m+3}.
AB,
∴ ![]() ,
,
解得1≤m≤2.
∴实数m的取值范围是[1,2]
(2)解:∵A∩B=B,∴BA,
①当B=时,贼》3m+2,∴m<﹣3符合题意;
②当B≠时, 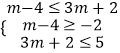 ,无解.
,无解.
综上可得,m<﹣3.
∴实数m的取值范围是(﹣∞,﹣3)
【解析】(1)由AB,列出不等式组,即可求解实数m的取值范围.(2)由A∩B=B,根据B=和B≠分类讨论,分别求解实数m的取值范围,取并集即可求解m的取值范围.
【考点精析】利用集合的交集运算对题目进行判断即可得到答案,需要熟知交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立.
B,反之也成立.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(Ⅰ)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 恒过的定点
恒过的定点![]() 的坐标;
的坐标;
(Ⅱ)在(Ⅰ)的条件下,若![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱世杰是历史上最未打的数学家之一,他所著的《四元玉鉴》卷中“如像招数一五间”,有如下问题:“今有官司差夫一千八百六十四人筑堤,只云初日差六十四人,次日转多七人,每人日支米三升,共支米四百三石九斗二升,问筑堤几日?”.其大意为:“官府陆续派遣1864人前往修筑堤坝,第一天派出64人,从第二天开始,每天派出的人数比前一天多7人,修筑堤坝的每人每天发大米3升,共发出大米40392升,问修筑堤坝多少天”.在这个问题中,前5天应发大米( )
A. 894升 B. 1170升 C. 1275升 D. 1457升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名同学在5次英语口语测试中的成绩统计如图的茎叶图所示.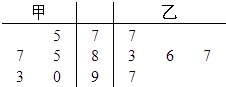
(注:样本数据x1 , x2 , …,xn的方差s2= ![]() [
[ ![]() +
+ ![]() +…+
+…+ ![]() ],其中
],其中 ![]() 表示样本均值)
表示样本均值)
(1)现要从中选派一人参加英语口语竞赛,从两同学的平均成绩和方差分析,派谁参加更合适;
(2)若将频率视为概率,对学生甲在今后的三次英语口语竞赛成绩进行预测,记这三次成绩中高于80分的次数为ξ,求ξ的分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在[1,+∞)上的函数f(x)=  给出下列结论:
给出下列结论:
①函数f(x)的值域为(0,8];
②对任意的n∈N,都有f(2n)=23﹣n;
③存在k∈( ![]() ,
, ![]() ),使得直线y=kx与函数y=f(x)的图象有5个公共点;
),使得直线y=kx与函数y=f(x)的图象有5个公共点;
④“函数f(x)在区间(a,b)上单调递减”的充要条件是“存在n∈N,使得(a,b)(2n , 2n+1)”
其中正确命题的序号是( )
A.①②③
B.①③④
C.①②④
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的上下两个焦点分别为
的上下两个焦点分别为![]() ,
, ![]() ,过点
,过点![]() 与
与![]() 轴垂直的直线交椭圆
轴垂直的直线交椭圆![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 的面积为
的面积为![]() ,椭圆
,椭圆![]() 的离心力为
的离心力为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知![]() 为坐标原点,直线
为坐标原点,直线![]() :
: ![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() ,
, ![]() 两个不同的点,若存在实数
两个不同的点,若存在实数![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com