
【题目】已知函数f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)当a>0时,求函数f(x)的单调区间;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
【答案】(1)见解析(2)5.
【解析】试题分析:(1)先求导数,转化研究二次函数![]() 符号变化规律:当判别式非正时,导函数不变号;当判别式大于零时,定义域上有两个根 ,导函数符号先负再正再负(2)先利用参变分离法化简不等式得
符号变化规律:当判别式非正时,导函数不变号;当判别式大于零时,定义域上有两个根 ,导函数符号先负再正再负(2)先利用参变分离法化简不等式得![]() ,转化求函数
,转化求函数![]() 最小值,利用导数可得
最小值,利用导数可得![]() 有唯一极小值,也是最小值,再根据极点条件求最小值取值范围,进而可得a的最小值.
有唯一极小值,也是最小值,再根据极点条件求最小值取值范围,进而可得a的最小值.
试题解析: 解 (1)f′(x)=![]() ,x>-1.
,x>-1.
当a≥![]() 时,f′(x)≤0,∴f(x)在(-1,+∞)上单调递减.
时,f′(x)≤0,∴f(x)在(-1,+∞)上单调递减.
当0<a<![]() 时,
时,
当-1<x<![]() 时,f′(x)<0,f(x)单调递减;
时,f′(x)<0,f(x)单调递减;
当![]() <x<
<x<![]() 时,f′(x)>0,f(x)单调递增;
时,f′(x)>0,f(x)单调递增;
当x>![]() 时,f′(x)<0,f(x)单调递减.
时,f′(x)<0,f(x)单调递减.
综上,当a≥![]() 时,f(x)的单调递减区间为(-1,+∞);
时,f(x)的单调递减区间为(-1,+∞);
当0<a<![]() 时,f(x)的单调递减区间为
时,f(x)的单调递减区间为![]() ,
,![]() ,
,
f(x)的单调递增区间为![]() .
.
(2)原式等价于ax>(x+1)ln (x+1)+2x+1,
即存在x>0,使![]() 成立.
成立.
设![]() ,x>0,
,x>0,
则![]() ,x>0,
,x>0,
设h(x)=x-1-ln (x+1),x>0,
则h′(x)=1-![]() >0,∴h(x)在(0,+∞)上单调递增.
>0,∴h(x)在(0,+∞)上单调递增.
又h(2)<0,h(3)>0,根据零点存在性定理,可知h(x)在(0,+∞)上有唯一零点,设该零点为x0,则x0-1=ln (x0+1),且x0∈(2,3),
∴![]()
又a>x0+2,a∈Z,∴a的最小值为5.


科目:高中数学 来源: 题型:
【题目】已知A,B,C为锐角△ABC的内角, ![]() =(sinA,sinBsinC),
=(sinA,sinBsinC), ![]() =(1,﹣2),
=(1,﹣2), ![]() ⊥
⊥ ![]() .
.
(1)tanB,tanBtanC,tanC能否构成等差数列?并证明你的结论;
(2)求tanAtanBtanC的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=![]() ,AC=3, BC=2,P是△ABC内的一点.
,AC=3, BC=2,P是△ABC内的一点.
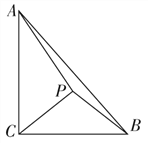
(1)若P是等腰直角三角形PBC的直角顶点,求PA的长;
(2)若∠BPC=![]() ,设∠PCB=θ,求△PBC的面积S(θ)的解析式,并求S(θ)的最大值.
,设∠PCB=θ,求△PBC的面积S(θ)的解析式,并求S(θ)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=AD=2DC=2 ![]() ,PA=4且E为PB的中点.
,PA=4且E为PB的中点. 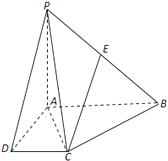
(1)求证:CE∥平面PAD;
(2)求直线CE与平面PAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数 ![]() 在(0,+∞)上为增函数,g(x)=f(x)+2
在(0,+∞)上为增函数,g(x)=f(x)+2 ![]()
(1)求m的值,并确定f(x)的解析式;
(2)对于任意x∈[1,2],都存在x1 , x2∈[1,2],使得f(x)≤f(x1),g(x)≤g(x2),若f(x1)=g(x2),求实数t的值;
(3)若2xh(2x)+λh(x)≥0对于一切x∈[1,2]成成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:
(Ⅰ)该顾客中奖的概率;
(Ⅱ)该顾客获得的奖品总价值ξ(元)的概率分布列和期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为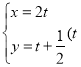 为参数),直线
为参数),直线![]() 和圆
和圆![]() 交于
交于![]() 两点,
两点,![]() 是圆
是圆![]() 上不同于
上不同于![]() 的任意一点.
的任意一点.
(1)求圆心的极坐标;
(2)求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com