
【题目】定义域为![]() 的单调函数
的单调函数![]() 满足
满足![]()
![]() ,且
,且![]() ,
,
(1)求![]() ,
,![]() ;
;
(2)判断函数![]() 的奇偶性,并证明;
的奇偶性,并证明;
(3)若对于任意![]() 都有
都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为a,
的棱长为a,![]() 分别是棱
分别是棱![]() 、
、![]() 的中点,过点
的中点,过点![]() 的平面分别与棱
的平面分别与棱![]() 、
、![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() ,给出以下四个命题:
,给出以下四个命题:
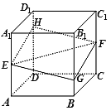
(1)平面![]() 与平面
与平面![]() 所成角的最大值为
所成角的最大值为![]() ;
;
(2)四边形![]() 的面积的最小值为
的面积的最小值为![]() ;
;
(3)四棱锥![]() 的体积为
的体积为![]() ;
;
(4)点![]() 到平面
到平面![]() 的距离的最大值为
的距离的最大值为![]() ,
,
其中正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台为宣传本省,随机对本省内15~65岁的人群抽取了![]() 人,回答问题“本省内著名旅游景点有哪些”统计结果如图表所示.
人,回答问题“本省内著名旅游景点有哪些”统计结果如图表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 |
|
|
|
第2组 |
| 18 |
|
第3组 |
|
|
|
第4组 |
|
|
|
第5组 |
|
|
|

(1)分别求出![]() 的值;
的值;
(2)从第2、3、4组回答正确的人中用分层抽样的方法抽取6人,求第2、3、4组每组各抽取多少人?
(3)指出直方图中,这组数据的中位数是多少(取整数值)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊数学家阿波罗尼奧斯(约公元前262~公元前190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,他证明过这样一个命题:平面内与两定点距离的比为常数k(k>0,k≠1)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.在平面直角坐标系中,设A(﹣3,0),B(3,0),动点M满足![]() =2,则动点M的轨迹方程为()
=2,则动点M的轨迹方程为()
A. (x﹣5)2+y2=16B. x2+(y﹣5)2=9
C. (x+5)2+y2=16D. x2+(y+5)2=9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,⊙O1与⊙O2交于P、Q两点,⊙A的弦以与⊙O2相切,⊙O2的弦PB与⊙O1相切,直线PQ与△PAB的外接圆⊙O交于另一点R.证明:PQ=QR.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:kx-y+4=0与直线l2:x+ky-3=0相交于点P,则当实数k变化时,点P到直线4x-3y+10=0的距离的最大值为( )
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:y=kx+m与椭圆![]() +
+![]() =1(a>b>0)恰有一个公共点P,l与圆x2+y2=a2相交于A,B两点.
=1(a>b>0)恰有一个公共点P,l与圆x2+y2=a2相交于A,B两点.
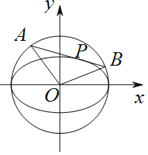
(Ⅰ)求m(用a,b,k表示);
(Ⅱ)当k=-![]() 时,△AOB的面积的最大值为
时,△AOB的面积的最大值为![]() a2,求椭圆的离心率.
a2,求椭圆的离心率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知数列![]() 中,
中,![]() ,前项和
,前项和![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列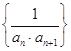 的前项和为
的前项和为![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 对一切正整数都成立?若存在,求出
对一切正整数都成立?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com