
【题目】已知圆![]() ,点
,点![]() 在圆内,在过点P所作的圆的所有弦中,弦长最小值为
在圆内,在过点P所作的圆的所有弦中,弦长最小值为![]() .
.
(1)求实数a的值;
(2)若点M为圆外的动点,过点M向圆C所作的两条切线始终互相垂直,求点M的轨迹方程.
【答案】(1)![]() 或4;(2)
或4;(2)![]() 或
或![]() .
.
【解析】
(1)由题点P与圆心的连线与弦垂直,即点P为弦的中点时,过点P的弦长最短.再根据垂径定理求解实数a的值即可.
(2)根据圆的性质可得点M的轨迹为![]() 为圆心,以
为圆心,以![]() 为半径的圆,再根据(1)中的两种情况求解即可.
为半径的圆,再根据(1)中的两种情况求解即可.
(1)由圆![]()
得到圆心坐标为![]()
点![]() 在圆内,
在圆内,
所以![]()
解得![]() ,
,
由圆的弦的性质可知,点P与圆心的连线与弦垂直,
即点P为弦的中点时,过点P的弦长最短
在过点P所作的圆的所有弦中,弦长最小值为![]() .
.
所以![]() ,
,
解得![]() 或4,(符合
或4,(符合![]() ).
).
(2)由(1)可知,![]() 或
或![]() 时,因为过点M向圆C作的两条切线总互相垂直,所以由圆的切线的性质可知两条切线和垂直于切线的两条半径构成的四边形为正方形,
时,因为过点M向圆C作的两条切线总互相垂直,所以由圆的切线的性质可知两条切线和垂直于切线的两条半径构成的四边形为正方形,
且边长为![]() ,对角线长为
,对角线长为![]() ,
,
所以,点M的轨迹为![]() 为圆心,以
为圆心,以![]() 为半径的圆
为半径的圆
所以点M的轨迹方程为
![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某班级在一次数学竞赛中为全班学生设置了一等奖、二等奖、三等奖以及参与奖,各个奖品的单价分别为:一等奖![]() 元、二等奖
元、二等奖![]() 元、三等奖
元、三等奖![]() 元、参与奖
元、参与奖![]() 元,获奖人数的分配情况如图,则以下说法不正确的是( ).
元,获奖人数的分配情况如图,则以下说法不正确的是( ).
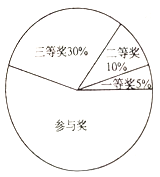
A. 获得参与奖的人数最多
B. 各个奖项中参与奖的总费用最高
C. 购买每件奖品费用的平均数为![]() 元
元
D. 购买的三等奖的奖品件数是一、二等奖的奖品件数和的二倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,下顶点为
,下顶点为![]() ,椭圆
,椭圆![]() 的离心率是
的离心率是![]() ,
,![]() 的面积是
的面积是![]() .
.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() 点),若直线
点),若直线![]() 与直线
与直线![]() 的斜率之和为1,证明:直线
的斜率之和为1,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 作垂直于
作垂直于![]() 轴的直线与抛物线交于
轴的直线与抛物线交于![]() ,
,![]() 两点,且以线段
两点,且以线段![]() 为直径的圆过点
为直径的圆过点![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 为曲线
为曲线![]() :
:![]() 上的动点,求
上的动点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在抽取彩票“双色球”中奖号码时,有33个红色球,每个球的编号分别为01,02,…,33.一位彩民用随机数表法选取6个号码作为6个红色球的编号,选取方法是从下面的随机数表中第1行第6列的数字3开始,从左向右读数,则依次选出的第3个红色球的编号为( )
49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64 |
57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 |
A.21B.32C.09D.20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,椭圆
,椭圆![]() 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且线段
,且线段![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() ,求点
,求点![]() 横坐标的取值范围.
横坐标的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com