
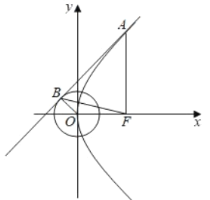
【题目】已知抛物线![]() :
:![]() ,圆
,圆![]() :
:![]() ,直线
,直线![]() :
:![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() ,且与圆
,且与圆![]() 相切于点
相切于点![]() .
.
(1)当![]() ,
,![]() 时,求直线
时,求直线![]() 方程与抛物线
方程与抛物线![]() 的方程;
的方程;
(2)设![]() 为抛物线
为抛物线![]() 的焦点,
的焦点,![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,当
,当![]() 取得最大值时,求实数
取得最大值时,求实数![]() 的值.
的值.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角),以坐标原点
的倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 时直线
时直线![]() 的普通方程;
的普通方程;
(2)直线![]() 和曲线
和曲线![]() 交于两点
交于两点![]() ,点
,点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
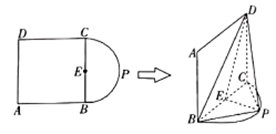
【题目】如图,![]() 是正方形,点
是正方形,点![]() 在以
在以![]() 为直径的半圆弧上(
为直径的半圆弧上(![]() 不与
不与![]() ,
,![]() 重合),
重合),![]() 为线段
为线段![]() 的中点,现将正方形
的中点,现将正方形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
(1)证明:![]() 平面
平面![]() .
.
(2)若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,求
的体积最大时,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
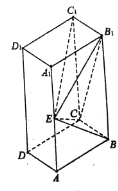
【题目】如图,已知四棱柱![]() 的底面
的底面![]() 是正方形,侧面
是正方形,侧面![]() 是矩形,
是矩形,![]() ,
,![]() 为
为![]() 的中点,平面
的中点,平面![]() 平面
平面![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)判断二面角![]() 是否为直二面角,不用说明理由;
是否为直二面角,不用说明理由;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国仓储指数是反映仓储行业经营和国内市场主要商品供求状况与变化趋势的一套指数体系.如图所示的折线图是2017年和2018年的中国仓储指数走势情况.根据该折线图,下列结论中不正确的是( )

A. 2018年1月至4月的仓储指数比2017年同期波动性更大
B. 2017年、2018年的最大仓储指数都出现在4月份
C. 2018年全年仓储指数平均值明显低于2017年
D. 2018年各月仓储指数的中位数与2017年各月仓储指数中位数差异明显
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() ,
,![]() ,
,![]() 的中点.
的中点.

(I)证明:直线![]() 与
与![]() 共面;
共面;
(Ⅱ)证明:平面![]() 平面
平面![]() ;并试写出
;并试写出![]() 到平面
到平面![]() 的距离(不必写出计算过程).
的距离(不必写出计算过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】西湖小学为了丰富学生的课余生活开设课后少年宫活动,其中面向二年级的学生共开设了三门课外活动课:七巧板、健美操、剪纸.203班有包括奔奔、果果在内的5位同学报名参加了少年宫活动,每位同学只能挑选一门课外活动课,已知每门课都有人选,则奔奔和果果选择了同一个课外活动课的选课方法种数为( )
A.18B.36C.72D.144
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com