
| A. | $\frac{33}{4}$ | B. | $\frac{25}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{{\sqrt{17}}}{4}$ |
分析 展开,并根据x+y=1可以得到$z=xy+\frac{2}{xy}-2$,可令t=xy,并求出$t∈(0,\frac{1}{4}]$,而根据$f(t)=t+\frac{2}{t}$的单调性即可求出f(t)的最小值,进而求出z的最小值.
解答 解:z=$(x+\frac{1}{x})(y+\frac{1}{y})$
=$xy+\frac{1}{xy}+\frac{y}{x}+\frac{x}{y}$
=$xy+\frac{1}{xy}+\frac{(x+y)^{2}-2xy}{xy}$
=$xy+\frac{2}{xy}-2$;
令t=xy,则$0<t=xy≤{(\frac{x+y}{2})^2}=\frac{1}{4}$;
由$f(t)=t+\frac{2}{t}$在$({0,\frac{1}{4}}]$上单调递减,故当t=$\frac{1}{4}$时 $f(t)=t+\frac{2}{t}$有最小值$\frac{33}{4}$,
即:$x=y=\frac{1}{2}$时z有最小值$\frac{25}{4}$.
故选B.
点评 考查基本不等式的应用,注意等号成立的条件,要熟悉函数$f(x)=x+\frac{a}{x}(a>0)$的单调性.


科目:高中数学 来源: 题型:解答题
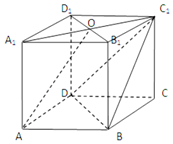 如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1与B1D1的交点,已知AA1=AB=2,∠BAD=60°;
如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1与B1D1的交点,已知AA1=AB=2,∠BAD=60°;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 30 | C. | 40 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图一个水平放置的无盖透明的正方体容器,高12cm,将一个球放在容器口,在向容器内注水,当球面恰好接触水面时测得水深为8cm,如果不计容器厚度,则球的体积为$\frac{2197π}{6}$cm3.
如图一个水平放置的无盖透明的正方体容器,高12cm,将一个球放在容器口,在向容器内注水,当球面恰好接触水面时测得水深为8cm,如果不计容器厚度,则球的体积为$\frac{2197π}{6}$cm3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
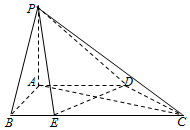 如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,PA⊥平面ABCD,点E在BC上,BC=2AB=2AD=4BE.
如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,PA⊥平面ABCD,点E在BC上,BC=2AB=2AD=4BE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com