
【题目】中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)的一种,现有十二生肖的吉祥物各一个,甲、乙、丙三位同学依次选一个作为礼物,甲同学喜欢牛、马和羊,乙同学喜欢牛、兔、狗和羊,丙同学哪个吉祥物都喜欢,则让三位同学选取的礼物都满意的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】心理学研究表明,人极易受情绪的影响,某选手参加7局4胜制的兵乒球比赛.
(1)在不受情绪的影响下,该选手每局获胜的概率为![]() ;但实际上,如果前一句获胜的话,此选手该局获胜的概率可提升到
;但实际上,如果前一句获胜的话,此选手该局获胜的概率可提升到![]() ;而如果前一局失利的话,此选手该局获胜的概率则降为
;而如果前一局失利的话,此选手该局获胜的概率则降为![]() ,求该选手在前3局获胜局数
,求该选手在前3局获胜局数![]() 的分布列及数学期望;
的分布列及数学期望;
(2)假设选手的三局比赛结果互不影响,且三局比赛获胜的概率为![]() ,记
,记![]() 为锐角
为锐角![]() 的内角,求证:
的内角,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且sin2A+sin2B+sin2C=sinAsinB+sinBsinC+sinCsin A.
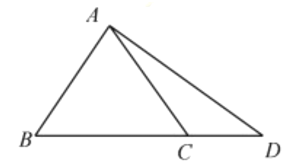
(1)证明:△ABC是正三角形;
(2)如图,点D在边BC的延长线上,且BC=2CD,AD![]() ,求sin∠BAD的值.
,求sin∠BAD的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为贯彻执行党中央“不忘初心,牢记使命”主题教育活动,增强企业的凝聚力和竞争力。某重装企业的装配分厂举行装配工人技术大比武,根据以往技术资料统计,某工人装配第n件工件所用的时间(单位:分钟)![]() 大致服从的关系为
大致服从的关系为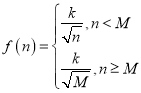 (k、M为常数).已知该工人装配第9件工件用时20分钟,装配第M件工件用时12分钟,那么可大致推出该工人装配第4件工件所用时间是( )
(k、M为常数).已知该工人装配第9件工件用时20分钟,装配第M件工件用时12分钟,那么可大致推出该工人装配第4件工件所用时间是( )
A.40分钟B.35分钟C.30分钟D.25分钟
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了了解年研发资金投人量![]() (单位:亿元)对年销售额
(单位:亿元)对年销售额![]() (单位:亿元)的影响.对公司近
(单位:亿元)的影响.对公司近![]() 年的年研发资金投入量
年的年研发资金投入量![]() 和年销售额
和年销售额![]() 的数据,进行了对比分析,建立了两个函数模型:①
的数据,进行了对比分析,建立了两个函数模型:①![]() ,②
,②![]() ,其中
,其中![]() 、
、![]() 、
、![]() 、
、![]() 均为常数,
均为常数,![]() 为自然对数的底数.并得到一些统计量的值.令
为自然对数的底数.并得到一些统计量的值.令![]() ,
,![]() ,经计算得如下数据:
,经计算得如下数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请从相关系数的角度,分析哪一个模型拟合程度更好?
(2)(ⅰ)根据(1)的选择及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(ⅱ)若下一年销售额![]() 需达到
需达到![]() 亿元,预测下一年的研发资金投入量
亿元,预测下一年的研发资金投入量![]() 是多少亿元?
是多少亿元?
附:①相关系数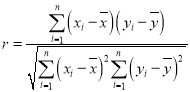 ,
,
回归直线![]() 中公式分别为:
中公式分别为: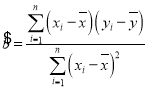 ,
,![]() ;
;
②参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为平面内一定点,动点
为平面内一定点,动点![]() 为平面内曲线
为平面内曲线![]() 上的任意一点,且满足
上的任意一点,且满足![]() ,过原点的直线交曲线
,过原点的直线交曲线![]() 于
于![]() 两点.
两点.
(1)证明:直线![]() 与直线
与直线![]() 的斜率之积为定值;
的斜率之积为定值;
(2)设直线![]() ,
,![]() 交直线
交直线![]() 于
于![]() 、
、![]() 两点,求线段
两点,求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在区间
,若存在区间![]() ,使得
,使得![]() ,则称函数
,则称函数![]() 为“可等域函数”,区间
为“可等域函数”,区间![]() 为函数
为函数![]() 的一个“可等域区间”.给出下列4个函数:
的一个“可等域区间”.给出下列4个函数:
①![]() ;②
;②![]() ; ③
; ③![]() ; ④
; ④![]() .
.
其中存在唯一“可等域区间”的“可等域函数”为( )
(A)①②③ (B)②③ (C)①③ (D)②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com