
分析 (1)令g(x)=x2+tx+2,要求函数f(x)的最小值,根据复合函数的单调性可知,只要求解函数g(x)的最小值即可,结合图象,需判断对称轴与区间[0,2]的位置关系,分类讨论;
(2)假设存在,则由已知等价于x2+tx+2=x在区间(0,2)上有两个不同的实根,分离参数,运用导数求出右边的最值和范围,即可得出结论.
解答 解:(1)令g(x)=x2+tx+2对称轴为x=-$\frac{t}{2}$,
①当-$\frac{t}{2}$≤0,即t≥0时,g(x)min=g(0)=2,∴f(x)min=lg2;
②当0<-$\frac{t}{2}$<2,即-4<t<0时,g(x)min=g(-$\frac{t}{2}$)=2-$\frac{{t}^{2}}{4}$,
考虑到g(x)>0,则
1°-2$\sqrt{2}$<t<0,f(x)min=f(-$\frac{t}{2}$)=lg(2-$\frac{{t}^{2}}{4}$),
2°-4<t≤-2$\sqrt{2}$,没有最小值.
③当-$\frac{t}{2}$≥2,即t≤-4时,g(x)min=g(2)=6+2t,
考虑到g(x)>0∴f(x)没有最小值.
综上所述:当t≤-2时f(x)没有最小值;
当t>-2时,f(x)min=$\left\{\begin{array}{l}{lg(2-\frac{{t}^{2}}{4}),-2\sqrt{2}<t<0}\\{lg2,0≤t<2\sqrt{2}}\end{array}\right.$.
(2)假设存在,则由已知等价于x2+tx+2=x在区间(0,2)上有两个不同的实根,
等价于t=-($\frac{2}{x}$+x)+1,x∈(0,2)
t′=-1+$\frac{2}{{x}^{2}}$,x∈(0,$\sqrt{2}$),t′>0;x∈($\sqrt{2}$,2),t′<0.
x=$\sqrt{2}$取最大值1-2$\sqrt{2}$.x=2,t=-2.
可得-2<t<1-2$\sqrt{2}$.
故存在,实数t的取值范围是-2<t<1-2$\sqrt{2}$.
点评 本题主要考查了对数函数定义域的求解,复合函数单调性的应用及二次函数在闭区间上的最值的求解,要注意考虑对称轴与区间位置关系的讨论,二次方程的实根分布问题的应用,本题的综合性比较强.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | $\frac{1}{3}$ | C. | -$\frac{7}{9}$ | D. | $-\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8m/s | B. | 10m/s | C. | 16m/s | D. | 18m/s |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
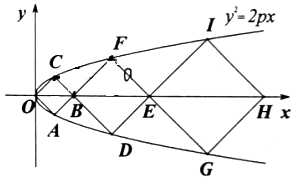 如图所示,O是坐标原点,三个正方形OABC、BDEF、EGHI的顶点中,O、A、C、D、F、G、I七个点都在抛物线y2=2px(p>0)上,另外,B、E、H三个点都在x轴上,则这三个正方形的面积之比( )
如图所示,O是坐标原点,三个正方形OABC、BDEF、EGHI的顶点中,O、A、C、D、F、G、I七个点都在抛物线y2=2px(p>0)上,另外,B、E、H三个点都在x轴上,则这三个正方形的面积之比( )| A. | 1:2:3 | B. | 1:4:9 | C. | 2:3:4 | D. | 4:9:16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com