练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在△ABC所在的平面上有一点P，满足
    BC
    =
    PA
    +
    PB
    +
    PC
    ．若△ABC的面积为12cm2，则△PBC的面积为
     
    cm2．
    考点：平面向量的基本定理及其意义
    专题：平面向量及应用
    分析：根据已知条件容易得到
    PA
    =-2
    PB
    ，所以P点在边AB上，且|
    PB
    |=
    1
    3
    |
    AB
    |    ，所以△PBC的面积是△ABC面积的
    1
    3
    ，这便可求出△PBC的面积．
    解答： 解：
    BC
    =
    PA
    +
    PB
    +
    PC
    ；
    ∴
    PC
    -
    PB
    =
    PA
    +
    PB
    +
    PC
    ；
    ∴
    PA
    =-2
    PB
    ；
    ∴如图所示，P点在边AB上，且|
    PB
    |=
    1
    3
    |
    AB
    |    ；
    ∴S△PBC=
    1
    3
    SABC=4    ．
    故答案为：4．
    点评：考查向量的减法运算：
    BC
    =
    PC
    -
    PB
    ，以及向量数乘的几何意义，共线向量基本定理，及三角形的面积公式．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如果变量x，y满足条件
    x-2y+4≤0
    x+2y-8≤0
    x≥0
    且z=3x+y，那么z的取值范围是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一个几何体的三视图如图所示，则该几何体的体积为（　　）
    A、7
    B、
    22
    3
    C、
    47
    6
    D、
    23
    3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（n）=
    n2(n=2k-1，k∈N*)
    -n2(n=2k，k∈N*)
    ，若an=f（n）+f（n+1），则a1+a2+a3+…+a2014=（　　）
    A、2013B、2014
    C、2015D、2016

    查看答案和解析>>

    科目：高中数学 来源： 题型：

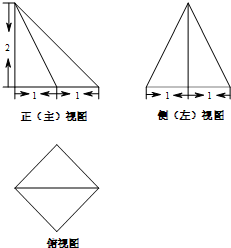    某四棱锥的三视图如图所示，其中正（主）视图是等腰直角三角形，侧（左）视图是等腰三角形，俯视图是正方形，则该四棱锥的体积是（　　）
    A、8
    B、
    8
    3
    C、4
    D、
    4
    3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若一个球的体积为
    9
    2
    π，则该球的表面积为（　　）
    A、
    2
    3
    π
    B、
    9
    2
    π
    C、18π
    D、9π

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知，|
    a
    |=|
    b
    |=2，
    a
    与
    b
    的夹角为
    π
    3
    ，则
    a
    +
    b
    在
    a
    上的投影为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

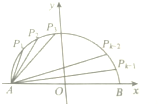    如图，AB是圆x2+y2=16的直径，把线段AB分成k（k≥4，k∈Z）等份，过每个分点作x轴的垂线交圆的上半部分于P1，P2，…，Pk-1，共k-1个点，令an=|APn|，n=1，2，3，…，k-1．则（　　）
    A、{an}是等差数列
    B、{an}是等比数列
    C、当k=8时，a12+a22+a32+…+a72=224
    D、当k=8时，a1+a2+a3+…+a7=224

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若二项式（ax-
    1
    x
    ）n的展开式的二项式系数的和为128，展开式的各项系数的和也为128，则展开式中
    1
    x3
    的系数是
     
    ．

    查看答案和解析>>

    同步练习册答案