
【题目】将一个骰子连续抛掷三次,它落地时向上的点数能组成成等差数列的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】已知a,b,c∈(0,+∞).
(1)若a=6,b=5,c=4是△ABC边BC,CA,AB的长,证明:cosA∈Q;
(2)若a,b,c分别是△ABC边BC,CA,AB的长,若a,b,c∈Q时,证明:cosA∈Q;
(3)若存在λ∈(-2,2)满足c2=a2+b2+λab,证明:a,b,c可以是一个三角形的三边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线C由上半椭圆C1: ![]() =1(a>b>0,y≥0)和部分抛物线C2:y=﹣x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1的离心率为
=1(a>b>0,y≥0)和部分抛物线C2:y=﹣x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1的离心率为 ![]() .
. 
(1)求a,b的值;
(2)过点B的直线l与C1 , C2分别交于点P,Q(均异于点A,B),若AP⊥AQ,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲、乙两个项目,对甲项目每投资10万元,一年后利润是1.2万元、1.18万元、1.17万元的概率分别为![]() ;已知乙项目的利润与产品价格的调整有关,在每次调整中,价格下降的概率都是p(0<p<1),设乙项目产品价格在一年内进行两次独立的调整.记乙项目产品价格在一年内的下降次数为X,对乙项目每投资10万元,X取0、1、2时,一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量X1、X2分别表示对甲、乙两项目各投资10万元一年后的利润.
;已知乙项目的利润与产品价格的调整有关,在每次调整中,价格下降的概率都是p(0<p<1),设乙项目产品价格在一年内进行两次独立的调整.记乙项目产品价格在一年内的下降次数为X,对乙项目每投资10万元,X取0、1、2时,一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量X1、X2分别表示对甲、乙两项目各投资10万元一年后的利润.
(1)求X1,X2的概率分布和均值E(X1),E(X2);
(2)当E(X1)<E(X2)时,求p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果![]() 的三个内角的正弦值分别等于
的三个内角的正弦值分别等于![]() 的三个内角的余弦值,则下列正确的是( )
的三个内角的余弦值,则下列正确的是( )
A. ![]() 与
与![]() 都是锐角三角形
都是锐角三角形
B. ![]() 与
与![]() 都是钝角三角形
都是钝角三角形
C. ![]() 是锐角三角形且
是锐角三角形且![]() 是钝角三角形
是钝角三角形
D. ![]() 是钝角三角形且
是钝角三角形且![]() 是锐角三角形
是锐角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是
是![]() 上的增函数.当实数
上的增函数.当实数![]() 取最大值时,若存在点
取最大值时,若存在点![]() ,使得过点
,使得过点![]() 的直线与曲线
的直线与曲线![]() 围成两个封闭图形,且这两个封闭图形的面积总相等,则点
围成两个封闭图形,且这两个封闭图形的面积总相等,则点![]() 的坐标为( )
的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分别直方图.
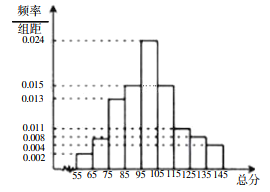
(1)求这100份数学试卷成绩的中位数;
(2)从总分在![]() 和
和![]() 的试卷中随机抽取2份试卷,求抽取的2份试卷中至少有一份总分少于65分的概率.
的试卷中随机抽取2份试卷,求抽取的2份试卷中至少有一份总分少于65分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区,规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m,经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO= ![]() .
. 
(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com